Example 1
Consider a bar of uniform cross-section shown in Fig. 3.1. The distributed force acting on the bar is varying linearly with x. Thus,
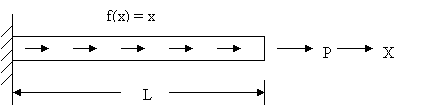
Figure 3.1
We choose the following numerical values of various geometric, material and force parameters.
| EA = 1, L = 1, P =10. |
(3.24) |
We choose a two-term approximation for the solution. Thus,
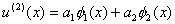 |
(3.25) |
where the basis functions are chosen to be the polynomials :
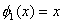 , , 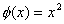 . . |
(3.26) |
Then, the derivatives of the basis functions are given by
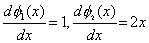 |
(3.27) |
Substituting the expressions (3.26) and values from equation (3.24), the expression for 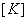 becomes becomes
Substituting the expressions (3.23) and (3.26) and values from equation (3.24), the expression for {F} takes the form :
{F} = 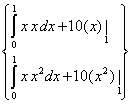 , ,
= 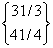 . . |
(3.29) |
Therefore, the matrix form of the algebraic equations (equation 3.16) becomes
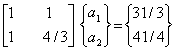 |
(3.30) |
The solution of this equation is given by
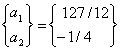 |
(3.31) |
Therefore, the approximate solution (equation 3.25) becomes
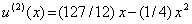 |
(3.32) |
To study the improvement in the accuracy of the solution, we consider the 3-term approximation next. Thus,
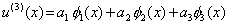 |
(3.33) |
where,
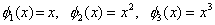 |
(3.34) |
The derivatives are given by
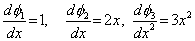 |
(3.35) |
Substituting the expressions (3.35) and values from (3.24), the 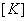 matrix becomes matrix becomes
 |
(3.36) |
Further, using the expressions (3.23) and (3.34) and the values from equation (3.24), the vector {F} becomes
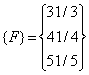 |
(3.37) |
Then, the matrix form (equation 3.16) of the algebraic equations become
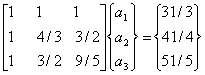 |
(3.38) |
The solution of above equation is
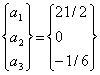 |
(3.39) |
Therefore, the approximate solution (equation 3.33) is given by
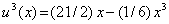 |
(3.40) |
For comparison purpose, the exact solution is needed. It can be found as follows. Substituting the expression for f from equation (3.23) and the values of EA , L and P from equation (3.24), the boundary value problem (equations 2.1a, 21b and 21c) becomes
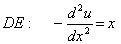 |
0 <x <1; |
(3.41a) |
BC : 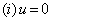 |
at x = 0, |
(3.41b) |
(ii) 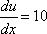 |
at x = 1 |
(3.41c) |
The solution of this problem is given by
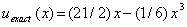 |
(3.42) |
Thus, it is seen that the 3-term approximation gives the exact solution. Substituting x =1 in equations (3.32) and (3.42), we get
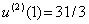 |
(3.43) |
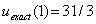 |
(3.44) |
Thus, the 2-term solution, although not exact, gives the exact value of the maximum displacement
|