Integral Forms Corresponding to a Point Force in the Interior of the Domain
Note that the integral formulations derived in Lecture 2 (equations 2.5b, 26 or 2.32 of Lecture 2) are not valid when there is a point force in the interior of the domain. For such a case, one needs to derive the corresponding integral formulations first. For this purpose, consider a more general problem shown in Fig. 3.2.
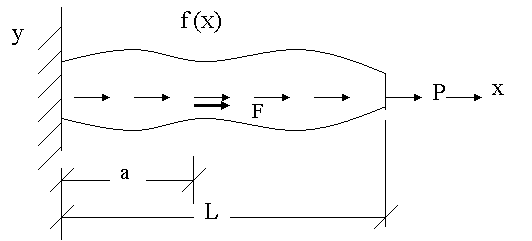
Figure 3.2
This problem is similar to the model boundary value problem described in section 2.1 except that now there is a point force at x = a . In this case, the derivative of u is not continuous at x = a . Therefore, the DE (equation 2.1a of Lecture 2) is not satisfied at the point x = a . Further, there is an additional condition that the jump in the derivative 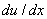 at x = a is proportional to the point force F at that point. Thus, the boundary value problem governing the axial displacement u is: at x = a is proportional to the point force F at that point. Thus, the boundary value problem governing the axial displacement u is:
| DE: |
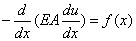 |
0 < x <a, a < x < L; |
(3.45a) |
| BC: |
(i) u = 0 |
at x = 0, |
(3.45b) |
| |
(ii) 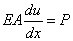 |
at x = L, |
(3.45c) |
| |
(iii) 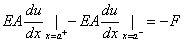 |
|
(3.45d) |
Integrating the weighted residue separately over the intervals (0,a) and (a,L) and carrying out the integration by parts we get
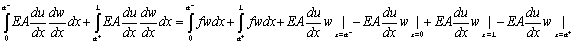 |
(3.46) |
Note that, even though du/dx is discontinuous at x = 0, it is integrable over the whole interval (0, L ). The other functions like dw / dx , w, f,A and E are also integrable over the interval (0, L ). Therefore, we combine the integrals over the intervals (0, a ) and ( a , L ) into a single integral over the interval (0, L )) on both sides of equation (3.46). Then, equation (3.46) becomes:
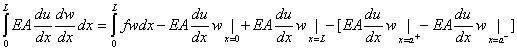 |
(3.47) |
Note that w = 0 at x = 0. Therefore, the 2 nd term on the right side of equation (3.47) becomes zero. Further, the 3 rd and 4 th terms of equation (3.47) can be expressed in terms of P and F using the boundary conditions (3.45c) and (3.45d) respectively. Then, equation (3.47) takes the from :
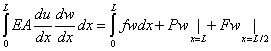 |
(3.48) |
This is the integral form used in weak or weighted residual formulation corresponding to the boundary value problem (3.45a), (3.45b), (3.45c) and (3.45d) shown in Fig. 3.2.
If instead of a single point force in the interior, there are m number of point forces acting at the points 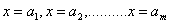 (Fig. 3.3), (Fig. 3.3),
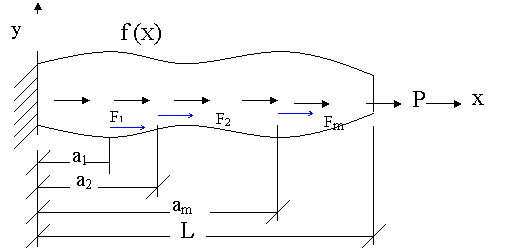
Figure 3.3
then the weak or weighted residual formulation takes the form:
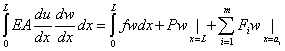 |
(3.49) |
The virtual work formulation of the boundary value problem (3.45a), (3.45b), (3.45c) and (3.45d) can be obtained by replacing the weight function w by the virtual displacement 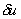 in equation (3.48): in equation (3.48):
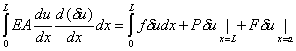 |
(3.50) |
The virtual work formulation corresponding to the problem of fig 3.3 is obtained similarly.
If we treat the symbol 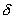 as the variational operator, and use its properties (equations 2.21-2.27), we get the variational functional as the variational operator, and use its properties (equations 2.21-2.27), we get the variational functional
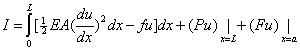 |
(3.51) |
that needs to be extremized to get the solution of the boundary value problem (3.45a), (3.45b), (3.45c) and (3.45d). This is the integral form of the variational formulation . The form corresponding to the problem of fig 3.3 is obtained similarly. Using the definition of 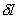 (equation 2.19 of Lecture 2), we get the following expression for (equation 2.19 of Lecture 2), we get the following expression for 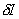 corresponding to the expression (51) : corresponding to the expression (51) :
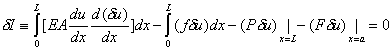 |
(3.52) |
|