Ritz Method
The variational functional I corresponding to the boundary value problem (2.1a), (2.1b) and (2.1c) is given by equation (2.32). The solution to the boundary value problem is obtained by extremising the functional I, that is, by setting the first variation of δI to zero. Using the expression (2.37) for δI, substituting δu/α for
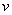 u and multiplying all the terms by α , we get u and multiplying all the terms by α , we get
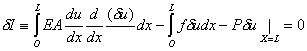 |
(3.1) |
Note that, using the above equation is equivalent to using the integral form corresponding to the virtual work formulation (equation 2.6) or the weighted residual (weak) formulation (equation 2.5b). While using the weighted residual formulations, however, one needs to choose an appropriate form for the weight function w also. This point is made clear in section 3.6
As stated in the introduction, in Ritz method, an approximate solution is assumed as a series of N terms of the following form :
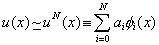 |
(3.2) |
where 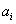 are unknown coefficients and are unknown coefficients and 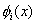 are a set of linearly independent functions of x defined over the interval [0,L]. The term "linear independence" means as follows. Consider a linear combination of are a set of linearly independent functions of x defined over the interval [0,L]. The term "linear independence" means as follows. Consider a linear combination of 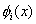 involving scalar coefficients involving scalar coefficients 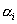 . If the only solution of the equation . If the only solution of the equation
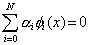 |
for x 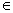 [0,L] [0,L] |
(3.3) |
is that all the coefficient are trivially zero, i.e.
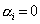 |
for i = 0,1...N, |
(3.4) |
then, the set of functions 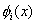 is said to be linearly independent over the interval [0,L]. The functions is said to be linearly independent over the interval [0,L]. The functions 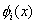 are called as the basis functions . Here, the basis functions are defined over the whole bar, i.e. for the interval [0,L]. Thus, they are called as the global basis functions. Later on, in finite element formulation, the (local) basis functions will be defined over a part of the element, called as an element. are called as the basis functions . Here, the basis functions are defined over the whole bar, i.e. for the interval [0,L]. Thus, they are called as the global basis functions. Later on, in finite element formulation, the (local) basis functions will be defined over a part of the element, called as an element.
When the weighted residual formulation is used, in general, the weight functions need not be the same as the basis functions. However, when both the sets are identical, this special case of the weighted residual formulation is called as the Galerkin formulation. This point is discussed in more details in section 3.6.
Note that the function 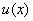 is required to satisfy the three admissibility conditions stated in section 2.6. These conditions impose certain restrictions on the basis functions is required to satisfy the three admissibility conditions stated in section 2.6. These conditions impose certain restrictions on the basis functions 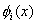 . The second condition implies that . The second condition implies that 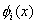 must be unconstrained at must be unconstrained at 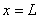 . The third condition requires that the derivatives . The third condition requires that the derivatives 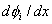 must be finite over the whole interval must be finite over the whole interval 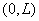 . The third restriction on the functions . The third restriction on the functions 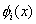 is imposed by the first admissibility condition that the form is imposed by the first admissibility condition that the form 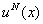 (expression 3.2) must satisfy the Dirichlet boundary condition (equation 2.1b). Then we get (expression 3.2) must satisfy the Dirichlet boundary condition (equation 2.1b). Then we get
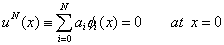 |
(3.5) |
If we assume that all 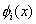 except except 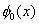 satisfy the condition satisfy the condition
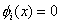 at x = 0 at x = 0 |
(3.6) |
then, from equation (3.5), we get
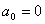 |
(3.7) |
Then, the series in expression (3.2) starts from i = 1 rather than form i = 0. Thus,
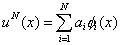 |
(3.8) |
where 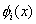 are linearly independent and satisfy the condition (3.6). are linearly independent and satisfy the condition (3.6).
Taking the variation of equation (3.2), we get
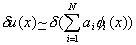 |
|
|
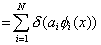 |
(property vii of section 2.5), |
|
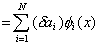 |
(property ii of section 2.5). (3.9) |
(3.9) |
Substituting the expression (3.9) for 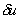 in equation (1), we get in equation (1), we get
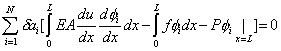 |
(3.10) |
Note that, in the above expression, each of the coefficients 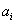 can be varied independently. That is, for given j, we can choose can be varied independently. That is, for given j, we can choose 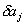 to be non zero and all the remaining to be non zero and all the remaining 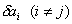 to be zero. Then, the above equation leads to the following set of equations: to be zero. Then, the above equation leads to the following set of equations:
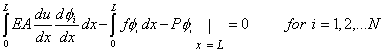 |
(3.11) |
Substituting the expression (3.8) for 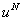 in equation (3.11) and changing the summation index from i to j, we get in equation (3.11) and changing the summation index from i to j, we get
Now define the following quantities :
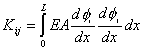 |
(3.13) |
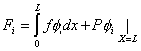 |
(3.14) |
Then, equation (3.12) becomes
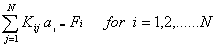 |
(3.15) |
In matrix form, this can be written as
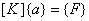 |
(3.16) |
Note that, if the functions 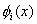 are non-dimensional, then the dimensions of the vectors are non-dimensional, then the dimensions of the vectors 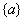 and and 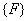 turn out to be that of the displacement and force respectively. Then, the dimension of turn out to be that of the displacement and force respectively. Then, the dimension of 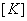 becomes that of stiffness (i.e. force per unit length). Therefore, becomes that of stiffness (i.e. force per unit length). Therefore, 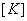 is called as the stiffness matrix, is called as the stiffness matrix, 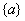 is called the displacement vector and is called the displacement vector and 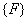 is called as the force vector. is called as the force vector.
The matrix 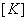 has the following properties. has the following properties.
- Expression (3.13) shows that
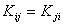 |
(3.17) |
Thus, the matrix 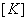 is symmetric. is symmetric.
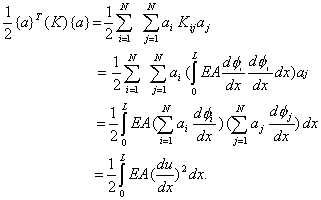 |
(3.18) |
Thus,
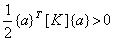 for any non-trivial vector for any non-trivial vector 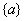 . . |
(3.19) |
Therefore, 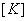 is a positive definite matrix. This implies that is a positive definite matrix. This implies that 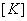 is invertible or is invertible or 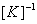 exists. Hence, exists. Hence,
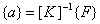 |
(3.20) |
Thus, Ritz method converts the differential equation of a boundary value problem into a set of algebraic equations using the corresponding integral form. Solution of the algebraic equations (equation 3.16) gives the coefficients of the assumed form of the solution (expression 3.8). Examples in the next section illustrate this procedure. These examples also show that, as the number of terms is increased, the solution becomes more accurate. It also illustrates that at the points of singularity in loading or geometric property (like A) or material property (like E), the accuracy is poor if only a few terms are chosen.
Amongst the many sets of linearly independent functions available, the set of polynomials offers a very simple and easy choice as far as the mathematical operations of Ritz method are concerned. Therefore, we choose 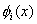 as the following set : as the following set :
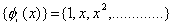 |
(3.21) |
But, 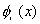 are supposed to satisfy the condition are supposed to satisfy the condition 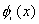 = 0 at x = 0. The first member of this set does not satisfy this condition. Therefore, we choose the set without the first function. Therefore = 0 at x = 0. The first member of this set does not satisfy this condition. Therefore, we choose the set without the first function. Therefore
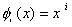 |
(3.22) |
Note that these functions satisfy all the constraints arising out of the three admissibility conditions required to be satisfied by 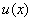 . .
|