Shape Functions
As stated earlier, we shall construct the shape functions directly in terms of the natural coordinates 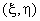 .Note that, for p = 1, i.e., for the first order or bi-linear Lagrangian approximation (eq. 24.6), the shape factions turn out to be the products of first degree 1-D polynomial in .Note that, for p = 1, i.e., for the first order or bi-linear Lagrangian approximation (eq. 24.6), the shape factions turn out to be the products of first degree 1-D polynomial in 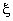 and first degree 1-D polynomial in and first degree 1-D polynomial in 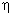 (eqs. 24.14-24.15). Similar thing happens for (eqs. 24.14-24.15). Similar thing happens for 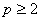 . Therefore, we follow a simpler procedure (somewhat) similar to the procedure adopted in Lecture 23 for obtaining the higher order Lagrangian shape functions for triangular elements. In this procedure : . Therefore, we follow a simpler procedure (somewhat) similar to the procedure adopted in Lecture 23 for obtaining the higher order Lagrangian shape functions for triangular elements. In this procedure :
- First, we express each shape function
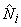 as a product of p -th degree 1-D polynomial in as a product of p -th degree 1-D polynomial in 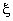 and p-th degree 1-D polynomial in and p-th degree 1-D polynomial in 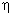 . .
- Then, we use the property of Lagrangian shape functions :
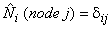 |
(25.4) |
to determine the coefficients in the expressions of 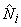 . .
For rectangular elements, another simple procedure of finding the shape functions exist. Note that, for p = 1, i.e., for the first order Lagrangian rectangular element, the shape functions turn out to be the tensor products of the 1-D linear Lagrangian shape functions in 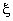 and and 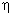 . Similar thing happens for . Similar thing happens for 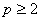 . For p -th order Lagrangian rectangular element, the shape functions turn out to be tensor products of the 1-D p -th order Lagrangian shape functions in . For p -th order Lagrangian rectangular element, the shape functions turn out to be tensor products of the 1-D p -th order Lagrangian shape functions in 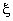 and and 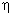 . Thus, we can adopt the following procedure : . Thus, we can adopt the following procedure :
- First, we express each shape function
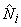 as the product of 1-D p-th order Lagrangian shape functions in as the product of 1-D p-th order Lagrangian shape functions in 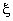 and and 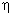 . Thus, . Thus,
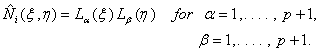 |
(25.5) |
- For chosen values of
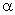 and and 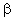 , the shape function index i is found from the property (25.4) of Lagrangian shape functions. , the shape function index i is found from the property (25.4) of Lagrangian shape functions.
The second order Lagrangian rectangular (master) element is shown in Fig. 25.3. As stated earlier, there are N = 9 nodes per element out of which N b = 8 are the boundary nodes and Ni = 1 is the internal node. Out of the 8 boundary nodes, 4 are placed at the vertices and the remaining 4 nodes are placed on the four boundaries with 1 node per boundary. To achieve proper variation of the primary variable, these nodes should not be close to the vertices. Instead, they should be closer to the boundary mid-points. In Fig. 25.3, they are placed at the boundary midpoints. The internal node is placed close to the centre of the element. In Fig. 25.3, it has been placed at the centre.
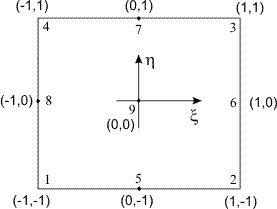
Figure 25.3 Second Order Lagrangian Rectangular (Master) Element
The shape functions of this element are :
where
are the 1-D quadratic Lagrangian shape functions given by equations (11.30-11.32).
The third order Lagrangian rectangular (master) element is shown in Fig. 25.4. As stated earlier, there are N = 16 nodes per element out of which N b = 12 are the boundary nodes Ni = 4 and are the internal nodes. Out of the 12 boundary nodes, 4 are placed at the vertices and the remaining 8 nodes are placed on the 4 boundaries, with 2 nodes per boundary. To achieve a proper variation of the primary variable, these 2 nodes should not be close to the vertices or to one another. In Fig. 25.4, they are placed such that they trisect the corresponding boundary. Similarly, 4 internal nodes should not be two close to the center or the boundaries. In Fig. 25.4, they are chosen in such a way that their 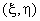 coordinates are coordinates are 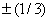 . .

Figure 25.4 Third Order Lagrangian Rectangular (Master) Element
The shape functions of this element are :
where
are the 1-D cubic Lagrangian shape functions.
|