Serendipity Rectangular Elements
Note that, for p-th order Lagrangian rectangular element, the number of nodes per element (N), the number of boundary nodes (Nb) and the number of internal nodes (Ni) are given by equations (25.1)-(25.3). Table 25.1 shows how N , Nb , Ni increase with p .
Table 25.1 Variation of Number of Nodes with Order of Approximation
p |
N |
Nb
|
Ni |
1 |
4 |
4 |
0 |
2 |
9 |
8 |
1 |
3 |
16 |
12 |
4 |
4 |
25 |
16 |
9 |
Table 25.1 shows that as p increases both N b and N i increase. Note that, an increase in Ni improves the order of approximation only over that particular element. However, an increase in Nb improves the order of approximation simultaneously over the neighboring element also. For Lagrangian rectangular elements, Ni becomes greater than Nb for 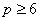 . Therefore, higher order Lagrangian rectangular element is not a good choice. It is desirable to have elements where the number of internal nodes ( N i ) is very small compared to the number of boundary ( Ni ), or if possible, zero. A family of rectangular elements with no internal nodes was discovered by an accident. Therefore, they are called as serendipity rectangular elements. . Therefore, higher order Lagrangian rectangular element is not a good choice. It is desirable to have elements where the number of internal nodes ( N i ) is very small compared to the number of boundary ( Ni ), or if possible, zero. A family of rectangular elements with no internal nodes was discovered by an accident. Therefore, they are called as serendipity rectangular elements.
Note that the simplest rectangular element of Lecture 24 has no internal nodes. Therefore, it is the first order serendipity rectangular element as well. To obtain the second order serendipity element from the second order Lagrangian element (Fig 25.3), we remove the internal node (i.e., the local node no. 9). This element is shown in Fig. 25.5.
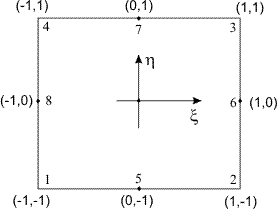
Figure 25.5 Second Order Serendipity Rectangular (Master) Element
The approximation for second order Lagrangian rectangular element having 9 nodes contains 9 terms which fall within the 2 nd parallelogram of the Pascal Triangle (Fig. 25.2). To obtain the approximation for second order serendipity element (Fig. 25.5) which has only 8 nodes, we need to remove one term form these 9 terms. This term must be symmetric in 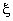 and and 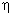 . We remove the term . We remove the term 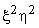 . Thus, the approximation becomes : . Thus, the approximation becomes :
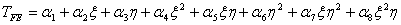 |
(25.10) |
To obtain the shape functions, we express each as 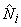 as : as :
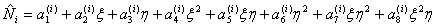 |
(25.11) |
Note that the degree of freedom per node, for serendipity elements, is also one. Therefore, the shape functions satisfy the property :
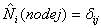 |
(25.12) |
This property is used to determine the unknown coefficients 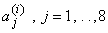 . This way, all the shape functions are determined. The shape functions are given by : . This way, all the shape functions are determined. The shape functions are given by :
Note that these shape functions cannot be expressed as tensor products of 1-D second order (or quadratic) Lagrangian shape functions in 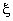 and and 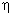 . .
The third order serendipity element is obtained from the third order Lagrangian rectangular element (Fig. 25.4) by removing the 4 internal nodes (i.e., the local node numbers 13, 14, 15 and 16). This element is shown in Fig. 25.5.
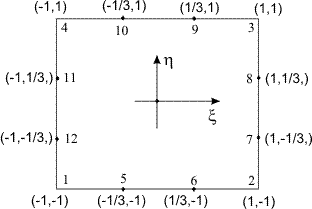
Figure 25.6 Third Order Serendipity Rectangular (Master) Element
The approximation for third order Lagrangian rectangular element having 16 nodes contains 16 terms that fall within the 3rd parallelogram of the Pascal Triangle (Fig. 25.2). To obtain the approximation for third order serendipity element (Fig. 25.5) which has only 12 nodes, we need to remove 4 terms from these 16 terms. The combination of these terms must be symmetric in 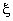 and and 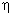 . We remove the following terms : . We remove the following terms : 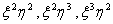 and and 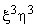 . Thus, the approximation contains the following terms : . Thus, the approximation contains the following terms : 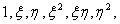 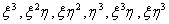 . To obtain the shape functions, we express each . To obtain the shape functions, we express each 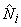 as as
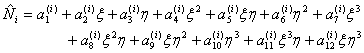 |
(25.14) |
The unknown coefficients 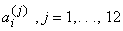 are determined from the shape function property (eq. 25.12). The shape functions are given by : are determined from the shape function property (eq. 25.12). The shape functions are given by :
|