Natural Coordinates
To facilitate numerical integration, we transform each (rectangular) element to a master (square) element for which the expression for numerical integration is available. The master element is a square of size two. This element is shown in Fig. 24.2. The coordinates 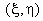 are called as natural coordinates. are called as natural coordinates.
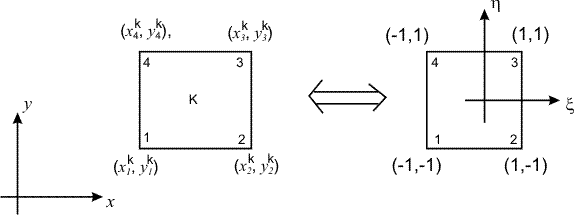
Figure 24.2 Mapping of a Rectangular Element onto the Master Element
Since the straight boundaries of a rectangular element parallel to (x, y) axes get mapped onto the straight boundaries of the master element parallel to 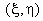 axes, the mapping can be expressed by the following relations : axes, the mapping can be expressed by the following relations :
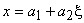
|
|
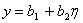 |
(24.2) |
Note that, x is independent of 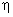 and y is independent of and y is independent of 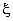 . To determine the unknown coefficients . To determine the unknown coefficients 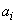 , we use the conditions that the nodes 1 and 2 of the rectangular element map onto the vertices (-1, -1) and (1, -1) respectively. Then, we get , we use the conditions that the nodes 1 and 2 of the rectangular element map onto the vertices (-1, -1) and (1, -1) respectively. Then, we get
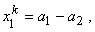
|
|
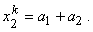 |
(24.3) |
By solving these equations, we obtain the following expressions for 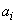 : :
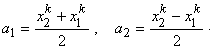 |
(24.4) |
Similarly, the unknown coefficients b i are determined form the conditions that the nodes 1 and 4 of the rectangular element map onto the vertices (-1, -1) and (-1, 1) respectively. Then, we get the following expressions for 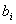 : :
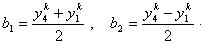 |
(24.5) |
After substituting the mapping function expression (eq. 24.2), the finite element approximation (eq. 24.1) becomes :
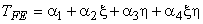 |
(24.6) |
where
Note that, this expression is also a bi-linear polynomial in 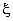 and and 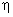 . .
|