Simplest Rectangular Element
Note that the simplest rectangular element has 4 nodes (at the vertices) with 1 dof per node. This element is shown is Fig. 24.1. The figure also shows the local node numbering system, the nodal coordinates 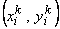 and the nodal degrees of freedom (dof) and the nodal degrees of freedom (dof) 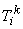 of local node i . The local node numbering system usually starts from bottom left corner and is counterclockwise. The notation for the coordinates and dof has the superscript k indicating that these quantities belong to the element k . This is called as local notation. of local node i . The local node numbering system usually starts from bottom left corner and is counterclockwise. The notation for the coordinates and dof has the superscript k indicating that these quantities belong to the element k . This is called as local notation.
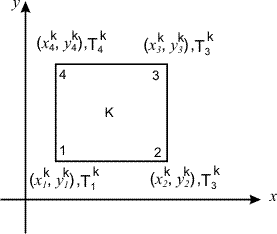
Figure 24.1 Four Noded Rectangular Element k
Since there are totally 4 dof per element, we need 4 linearly independent basis functions. We choose the lowest three monomial functions ( 1 , x, y ) and a second degree monomial function which is symmetric in x and y (i.e., xy ). Then the finite element approximation for k -th element becomes :
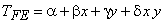 |
(24.1) |
and 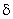 are unknown coefficients. Note that, it is a bi-linear polynomial in x and y . From this approximation, one can determine the shape function are unknown coefficients. Note that, it is a bi-linear polynomial in x and y . From this approximation, one can determine the shape function 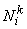 in terms of in terms of 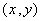 by using the properly by using the properly 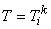 at at 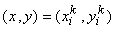 . However, for the purpose of numerical integration, the shape functions need to be transformed to the natural coordinates. Therefore, we first transform the approximation to the natural coordinates and then determine the shape functions in terms of the natural coordinates. . However, for the purpose of numerical integration, the shape functions need to be transformed to the natural coordinates. Therefore, we first transform the approximation to the natural coordinates and then determine the shape functions in terms of the natural coordinates.
|