Shape Functions in Natural Coordinates
To determine the shape functions, we evaluate T at the 4 nodes and use the following conditions :
Substituting these conditions in the approximation (24.6), we get the following equations:
Solving these equations, we obtain the following expressions for 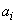 in terms of in terms of 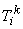 : :
Substituting the above expressions for 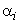 in the approximation (24.6) and rearranging the terms, we get in the approximation (24.6) and rearranging the terms, we get
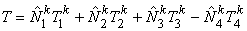 |
(24.11) |
where the shape functions 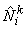 are given by : are given by :
Note that the shape factions 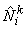 satisfy the following property : satisfy the following property :
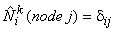 |
(24.13) |
These are called as bi-linear Lagrangian shape functions and the corresponding rectangular element is called as the first order Lagrangian rectangular element . Note that, the shape functions can also be expressed as :
where
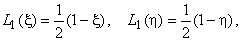
|
|
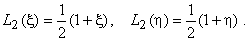 |
(24.15) |
Here, 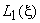 and and 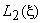 are the 1-D linear Lagrangian shape functions (eqs. 11.14-11.15) along the edges parallel to are the 1-D linear Lagrangian shape functions (eqs. 11.14-11.15) along the edges parallel to 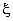 -axis. Similarly -axis. Similarly 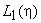 and and 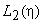 are the 1-D linear Lagrangian shape functions along the edges parallel to are the 1-D linear Lagrangian shape functions along the edges parallel to 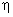 -axis. Thus, the bi-linear Lagrangian shape functions (of the first order Lagrangian rectangular element) can be constructed as tensor products of the 1-D 1 st order (i.e., linear) Lagrangian shape functions along the edges parallel to -axis. Thus, the bi-linear Lagrangian shape functions (of the first order Lagrangian rectangular element) can be constructed as tensor products of the 1-D 1 st order (i.e., linear) Lagrangian shape functions along the edges parallel to 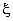 and and 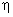 axes. axes.
|