Weak or Weighted Residual Formulation
Consider a function T ( x , y ), defined over the domain, which satisfies both the boundary conditions 20.3(b) and 20.3(c). In general, this function will not satisfy the differential equation 20.3(a). Instead, when T ( x , y ) is substituted in the left hand side of eq. 20.3(a), it will lead to the following error called as the residue and denoted by R ( x , y ) :
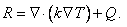 |
(20.4) |
To make the function T ( x , y ) an approximate solution of the problem (20.3(a), 20.3(b), 20.3(c)), we minimize the above residue by setting the integral of the product of R and a weight function w ( x , y ) to zero :
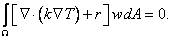 |
(20.5) |
The weight function w ( x , y ) must belong to a class of admissible functions. For the present problem, this class consists of the functions which satisfy the following conditions :
- On the boundary where T is specified, w must be zero. Thus, in the present problem, w = 0 on
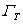 . .
- On the boundary where
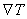 is specified, w must be unconstrained. Thus, in the present problem, w is unconstrained on is specified, w must be unconstrained. Thus, in the present problem, w is unconstrained on 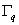 . .
- The function w should be smooth enough for the integral of the weighted residue to be finite.
We rewrite eq. (20.5) as :
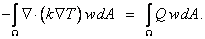 |
(20.6) |
To relax the smoothness requirements on the choice of the approximation function 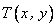 , we use a vector identity and the divergence theorem. The vector identity to be used is as follows. For a vector-valued function , we use a vector identity and the divergence theorem. The vector identity to be used is as follows. For a vector-valued function 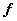 and a scalar- valued function g of the coordinates ( x , y ), the following relation holds : and a scalar- valued function g of the coordinates ( x , y ), the following relation holds :
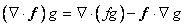 |
(20.7) |
The divergence theorem can be stated as follows. For a vector-valued function h of the coordinates, the area integral of 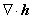 can be converted to the boundary integral using the following relation : can be converted to the boundary integral using the following relation :
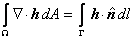 |
(20.8) |
where 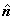 is the unit outward normal to the boundary is the unit outward normal to the boundary  of the domain of the domain  . .
Setting 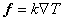 and g = w and using the identity (20.7), the left side of eq. (20.6) becomes : and g = w and using the identity (20.7), the left side of eq. (20.6) becomes :
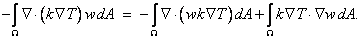 |
(20.9) |
Setting 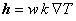 and using the divergence theorem (eq. 20.8) to convert the first right side integral to a boundary integral, eq. (20.9) can be expressed as : and using the divergence theorem (eq. 20.8) to convert the first right side integral to a boundary integral, eq. (20.9) can be expressed as :
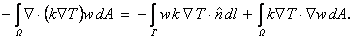 |
(20.10) |
Using eq. (20.1), the boundary integral on the right side of eq. (20.10) can be expressed in terms of the heat flux q . Further, since 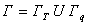 , the boundary integral can be split into two parts : (i) integral over , the boundary integral can be split into two parts : (i) integral over 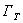 and (ii) integral over and (ii) integral over 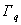 . With these simplifications, eq. (20.10) becomes : . With these simplifications, eq. (20.10) becomes :
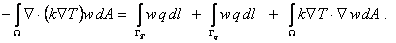 |
(20.11) |
Since w = 0 on 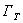 , the first boundary integral of the right side of eq. (20.11) becomes zero. Using the Neumann boundary condition 20.3(c), the second boundary integral can be expressed in terms of the specified heat flux , the first boundary integral of the right side of eq. (20.11) becomes zero. Using the Neumann boundary condition 20.3(c), the second boundary integral can be expressed in terms of the specified heat flux 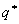 . With these simplifications, eq. (20.11) can be expressed as : . With these simplifications, eq. (20.11) can be expressed as :
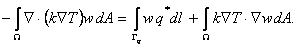 |
(20.12) |
Combining eqs. (20.6) and (20.12), and transposing the boundary integral to the other side, we get
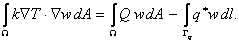 |
(20.13) |
This is called as the Weighted Residual Integral . This is the integral form used in the Weighted Residual Formulation. Now, the condition 3 of the class of admissible functions can be made explicit. For all the integrals of eq. (20.13) to be finite, 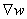 must be piecewise continuous over the domain must be piecewise continuous over the domain 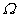 with only finite discontinuities. with only finite discontinuities.
|