Model Boundary Value Problem
To illustrate the development of integral formulations for 2-D problems, we consider the 2-D steady-state heat conduction problem. The domain  and its boundary and its boundary  are shown in Fig.20.1 are shown in Fig.20.1
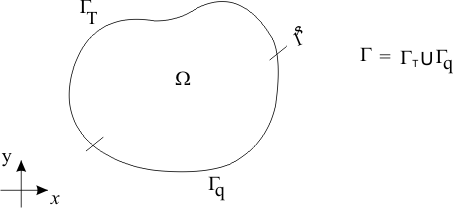
Fig.20.1 Domain and the Boundary of a model Boundary value problem
The thermal conductivity of the domain material is k and r(x, y) is the heat generated at point (x, y) per unit volume per unit time. A part of the boundary, denoted by  , is held at a temperature T* which can vary with the boundary coordinate s. The remaining part of the boundary, denoted by , is held at a temperature T* which can vary with the boundary coordinate s. The remaining part of the boundary, denoted by 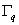 , receives the heat flux q* which also can vary with the boundary coordinate s. The heat flux q is defined as the heat flow (normal to the area) per unit area per unit time: , receives the heat flux q* which also can vary with the boundary coordinate s. The heat flux q is defined as the heat flow (normal to the area) per unit area per unit time:
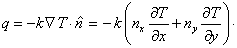 |
(20.1) |
Here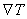 is the gradient of temperature T(x, y) and is the gradient of temperature T(x, y) and 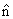 is the unit outward normal to the boundary. is the unit outward normal to the boundary. 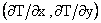 are the components of are the components of 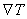 while while 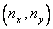 are the components of are the components of 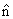 . If the quaintly q is positive, it means heat is flowing out of the domain and nice-versa. For steady problems, r, T* and q* are independent of time. . If the quaintly q is positive, it means heat is flowing out of the domain and nice-versa. For steady problems, r, T* and q* are independent of time.
Temperature T(x, y) at point (x, y) of the domain is governed by the following boundary value problem consisting of the differential equation (D.E.) and boundary condition (B.C.):
| D.E |
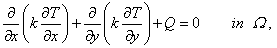 |
(20.2a) |
| B.C |
(i)  |
(20.2b) |
| |
(ii) 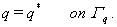 |
(20.2c) |
The differential equation 20.2(a) represents the heat balance of a small element of a domain. The boundary condition 20.2(b) is called as the Temperature or the Dirichet boundary condition where as the boundary condition 20.2(c) is called as the Heat Flux or Neumann boundary condition . Using the definition of divergence operator and eq. (20.1), the above problem can be expressed in vector notation:
| D.E. : |
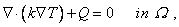 |
(20.3a) |
| B.C. |
(i)  |
(20.3b) |
| |
(ii)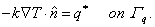 |
(20.3c) |
Here 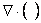 is the divergence operator. is the divergence operator.
|