| |
Variational Formulation
We obtain the other integral form in a similar fashion. Let 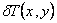 be a function which represents a small change in the function T (x , y) with the constraint that be a function which represents a small change in the function T (x , y) with the constraint that 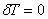 wherever T is specified. Thus, wherever T is specified. Thus, 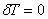 on the boundary on the boundary 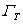 . Such a function is called as the variation of T and the operator . Such a function is called as the variation of T and the operator 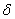 is called as the variational operator. Setting is called as the variational operator. Setting 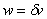 i n eq. (20.13), we get i n eq. (20.13), we get
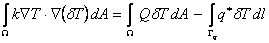 |
(20.14) |
Using the properties of 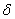 - operator from section 5 of Lecture 2 and assuming k to be independent of temperature, eq. (20.14) can be converted to the form : - operator from section 5 of Lecture 2 and assuming k to be independent of temperature, eq. (20.14) can be converted to the form :
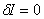 |
(20.15) |
where
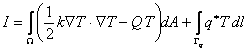 |
(20.16) |
The functional I is called as the Variational Functional of the boundary value problem (20.3(a), 20.3(b), 20.3(c)). This is the integral form to be used for the Variational Formulation . This integral needs to be extremized to obtain the solution of the boundary value problem.
The extremizing function T ( x , y ) needs to satisfy the following three conditions, which are similar to the conditions on the weight function w ( x , y ) :
- The function T ( x , y ) must satisfy the temperature boundary condition 20.3(b). Thus
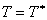 on on 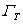 . Further, the variation . Further, the variation 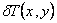 must satisfy the condition must satisfy the condition 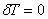 on on 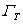 . .
- The function T ( x , y ) and its variation
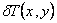 must be unconstrained where the heat flux boundary condition (eq. 20.3(c)) is specified. Thus, T and must be unconstrained where the heat flux boundary condition (eq. 20.3(c)) is specified. Thus, T and 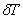 must be unconstrained on must be unconstrained on 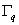
- The function T ( x , y ) must be smooth enough to make the functional I finite. Thus, T must be such that
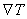 is finite at every point of the domain. is finite at every point of the domain.
The equation 20.3(a) is called as the Euler equation of the functional I (eq. 20.16). Further, the boundary condition 20.3(b) is called as the Essential boundary condition , and the condition 20.3(c) is called as the Natural boundary condition .
Variational functionals of the bar and beam problems represent the total potential energy of the system. However, the variational functional (eq. 20.16) of the heat condition problem has no such physical interpretation. Further, if the thermal conductivity k depends on temperature T , then the variational functional I may not exist, unless k is a specific function of T . However, the other integral form, namely the weighted residual integral (eq. 20.13) always exist.
|