Euler Equation and Natural Boundary Condition
To derive the Euler equation corresponding to the functional I (2.33), we proceed as follows. Let u be an admissible function which extremizes the functional. Then δu satisfies the condition that its value is zero at x = 0. Since v is equal to 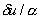 , , 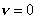 at x = 0. Note that the extremization condition (2.20) involves the expression for the functional I at at x = 0. Note that the extremization condition (2.20) involves the expression for the functional I at 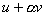 . Using expression (2.33), we get . Using expression (2.33), we get
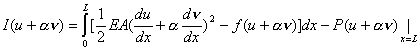 |
(2.34) |
Expanding the square term and separating the terms in the powers of 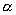 , we get: , we get:
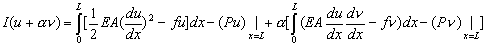
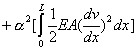 . . |
(2.35) |
Since, the first term on the right side of equation (2.35) is nothing but I(u), we get
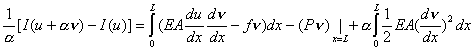 |
(2.36) |
Taking the limit as 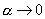 , we get , we get
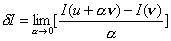
|
|
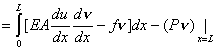 |
(2.37) |
Since the function u extremizes the functional I, 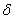 I = 0 . Therefore, we get I = 0 . Therefore, we get
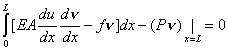 |
(2.38) |
for every
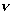 which satisfies the condition which satisfies the condition 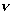 = 0 at x = 0. The extremizing function u is the solution of above equation. = 0 at x = 0. The extremizing function u is the solution of above equation.
To simplify the above equation, the first term is integrated by parts. Then, equation (2.38) becomes
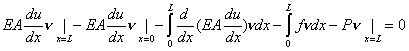 |
(2.39) |
Since 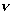 =0 at x = 0, the second term of equation (2.39) is zero. Combining the remaining two boundary terms and also the integral terms, we get =0 at x = 0, the second term of equation (2.39) is zero. Combining the remaining two boundary terms and also the integral terms, we get
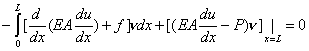 |
(2.40) |
Note that the above equation must be zero for a set of infinite functions 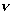 which satisfy the condition which satisfy the condition 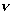 = 0 at x = 0 but otherwise are arbitrary. Let us first choose the following subset of this set, namely, the set of functions which are also zero at x = L. For such functions ( = 0 at x = 0 but otherwise are arbitrary. Let us first choose the following subset of this set, namely, the set of functions which are also zero at x = L. For such functions ( 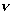 = 0 at x = L), equation (2.40) becomes = 0 at x = L), equation (2.40) becomes
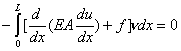 |
(2.41) |
Note that, equation (2.41) is true for every 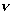 which is zero at x = 0 and L but otherwise is arbitrary. There are still infinite numbers of such functions. The only way in which equation (2.41) can be satisfied for such an infinite set of functions is that its integrand must be zero at every point of the interval [0, L]. In other words, the extremizing function u must satisfy the differential equation: which is zero at x = 0 and L but otherwise is arbitrary. There are still infinite numbers of such functions. The only way in which equation (2.41) can be satisfied for such an infinite set of functions is that its integrand must be zero at every point of the interval [0, L]. In other words, the extremizing function u must satisfy the differential equation:
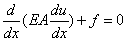 |
(2.42) |
which is same as equation (2.1a). Combining equations (2.40) and (2.41), the condition satisfied by u reduces to
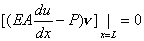 |
(2.43) |
Since, this condition is also true for an infinite number of functions, namely, a set of functions 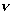 which satisfy the condition which satisfy the condition 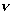 = 0 at x = 0 but otherwise are arbitrary, the only solution of equation (2.43) is = 0 at x = 0 but otherwise are arbitrary, the only solution of equation (2.43) is
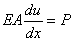 at x = L. at x = L. |
(2.44) |
This condition is same as the boundary condition (2.1c).
What we have shown is as follows. An admissible function u (i.e. a function u that satisfies the condition u = 0 at x = 0) which extremizes the functional I (expression 2.33) satisfies the DE (2.1a) (Called as the Euler equation) and the BC (2.1c) (called as the natural boundary condition).
|