Variational Formulation

Note that while deriving equation (2.6), it has been assumed that the function u satisfies both the boundary conditions (2.1b) and (2.1c). Additionally, if it is assumed that u also satisfies the differential equation (thereby making u the solution of the boundary value problem (2.1a), (2.1b) and (2.1c), equation (2.6) becomes:

Now, applying the properties of the variational operator 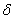, the first term becomes:

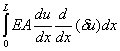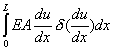	(Property iii)
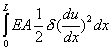	(Property i)
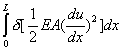	(Property ii)
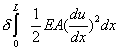	(Property iv)

Similarly, the second term becomes

,
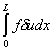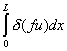,	(Property ii) ,
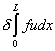	(Property iv)

Finally, the last terms becomes

,
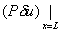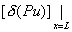,	(Property ii)
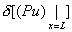	(Property iv)

Substitution of equations (2.29-2.31) into equation (2.28) leads to

Using property (vi), this becomes

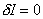(2.32)

where

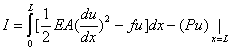(2.33)

Thus, we have proved the following result. The solution u of the boundary value problem (2.1a), (2.1b) and (2.1c) extremizes the functional I given by equation (2.33). The functional I is called the variational functional of the boundary value problem (2.1a), (2.1b) and (2.1c). Note that the functional (2.33) provides an integral form of the boundary value problem. The integral needs to be extremized to obtain the solution of the boundary value problem. This formulation is called as the Variational Formulation . Since it is derived from the virtual work formulation (equation 2.6), it is equivalent to the principle of virtual work. Like equation (2.6), this formulation also has a physical interpretation. Note that the quality I (expression 2.33) represents the total potential energy of the bar. Therefore, the variational formulation states the following principle. The solution of the boundary value problem (2.1a), (2.1b), and (2.1c) extremises the total potential energy of the bar. This is called as the Principal of the Stationary Value of the Total Potential Energy .

In the variational formulation, solution of the boundary value problem is obtained by extremizing the corresponding functional. While doing so, a set of admissible functions is chosen. The conditions which the extremizing function u is supposed to satisfy are similar to the conditions which the weight function w is expected to satisfy. These conditions are

1. The function u must satisfy the geometric or kinematic boundary conditions (equation 1b). Thus u = 0 at x = 0. Further, the variation δu must be 0 at this point.
2. The function u and its variation δu must be unconstrained where the force boundary condition is specified. Thus, u and d u are unconstrained at x = L.
3. The function u must be smooth enough to make the functional I finite. Thus, u must be such that du/dx is finite at every point of the interval (0, L).

If our starting point is the integral form given by the variational functional (2.33), rather than the differential form given by the boundary value problem (2.1a), (2.1b) and (2.1c), then it can be shown that the function u which extremizes the functional I (equation 2.33) actually satisfies the differential equation (2.1a). Thus, equation (2.1a) is called the Euler Equation of the functional I (equation 2.33). While extremizing the functional, the set of admissible functions is assumed to satisfy the geometric (or kinematic) boundary condition (equation 2.1b). Thus, equation (2.1b) is called as the Essential Boundary Condition . The condition at the other boundary (equation 2.1c) appears naturally while extremizing the functional I. Therefore, equation (2.1c) is called as the Natural Boundary Condition .