Variation and Extremum of a Functional
Consider a set of admissible functions on which a functional is defined. If one of the admissibility conditions is u = 0 at x = 0, then a typical function from this set can be represented as shown in Fig. 2.3(a).
| |
|
Figure 2.3 (a) |
Figure 2.3 (b) |
A small change in the argument of I is called as variation (or first variation) of u and is denoted by 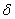 u. It is defined as a small change in the value of u at every point of the interval [0, L]. Note that u. It is defined as a small change in the value of u at every point of the interval [0, L]. Note that 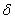 u is a function of x over the interval [0, L]. Since u is constrained at x = 0, no change is expected in u at x = 0. Therefore, the variation u is a function of x over the interval [0, L]. Since u is constrained at x = 0, no change is expected in u at x = 0. Therefore, the variation 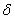 u takes the value zero at the end-point of the interval where u is specified. The function u takes the value zero at the end-point of the interval where u is specified. The function 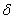 u is shown in Fig. 2.3(b). Since the value of u is shown in Fig. 2.3(b). Since the value of 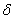 u is small everywhere, it is often expressed as u is small everywhere, it is often expressed as
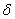 u = u = 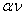 |
(2.17) |
where
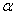 = a small number and = a small number and
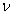 = an arbitrary function of x which satisfies the condition = an arbitrary function of x which satisfies the condition 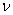 = 0 at x = 0. = 0 at x = 0.
This small change in the argument of I induces a change in the value of I. It is called as the variation (or first variation) of I and is denoted by 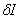 . To find the expressions of . To find the expressions of 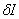 , we consider the value of the functional at the argument , we consider the value of the functional at the argument 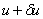 or or 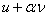 . Note that I( . Note that I( 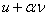 ) is a function of ) is a function of 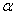 for given u and for given u and 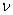 . Expanding . Expanding 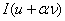 about about 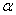 = 0, we get = 0, we get
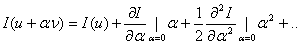 |
(2.18) |
The quantity 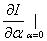 represents the variation represents the variation 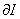 . Thus, . Thus,
The functional I is said to be extremum (minimum or maximum) when 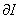 or or 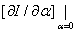 is zero. The corresponding extremizing function u is found from the condition is zero. The corresponding extremizing function u is found from the condition
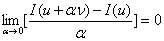 |
(2.20) |
for every function 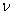 such that such that 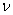 = 0 at x = 0 and = 0 at x = 0 and 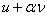 belongs to the set of admissible functions. belongs to the set of admissible functions.
While deriving the variational integral form from equation (2.6), some properties of the variational operator 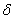 are needed. They are stated next. Note that are needed. They are stated next. Note that 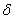 is an operator similar to the differential operator d operating on usual functions. So, the is an operator similar to the differential operator d operating on usual functions. So, the 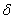 operator obeys certain properties of d operator like the product rule etc. Further, operator obeys certain properties of d operator like the product rule etc. Further, 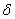 operator commutes with d operator, integral operator etc. the relevant properties needed in the derivation are: operator commutes with d operator, integral operator etc. the relevant properties needed in the derivation are:
| (i) |
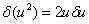 , ,
|
(2.21) |
| (ii) |
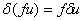 , (f is known function or a constant), , (f is known function or a constant),
|
(2.22) |
| (iii) |
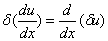 , ,
|
(2.23) |
| (iv) |
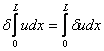 , ,
|
(2.24) |
| (v) |
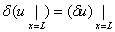 , ,
|
(2.25) |
| (vi) |
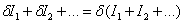 , ,
|
(2.26) |
| (vii) |
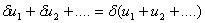
|
(2.27) |
|