| |
Functional
Functional is an operator, which operates on a function and returns a number. In other words, functional is a function which is defined over a set of functions and whose range is a set of numbers. The set of functions which constitute the domain of a functional is usually required to satisfy certain conditions on smoothness and/or on the values at the end - points of the interval. Such a set is called as a set or a class of admissible functions.
As an illustration of a functional, consider a set of functions u(x) which are functions of a single variable x for 0 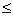 x x 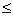 L, which have the value zero at x = 0 and which possess a continuous first derivative at all points of the interval [0, L]. Then, examples of functional are: L, which have the value zero at x = 0 and which possess a continuous first derivative at all points of the interval [0, L]. Then, examples of functional are:
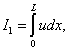 |
(2.10) |
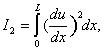 |
(2.11) |
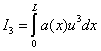 |
(a(x) is a known function), |
(2.12) |
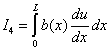 |
(b(x) is a known function), |
(2.13) |
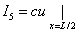 |
(c is a known number). |
(2.14) |
In each of the above examples, the operator 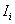 takes a function u(x) and returns a number either by integrating a quantity depending on u, takes a function u(x) and returns a number either by integrating a quantity depending on u, 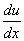 and some known functions or by evaluating u at some point of the interval. The integrand may involve higher derivatives of u or some functions of u like logarithmic, trigonometric, exponential etc or the power of u, its derivatives or its function. In classical books, a functional is often written as: and some known functions or by evaluating u at some point of the interval. The integrand may involve higher derivatives of u or some functions of u like logarithmic, trigonometric, exponential etc or the power of u, its derivatives or its function. In classical books, a functional is often written as:
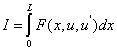 |
(2.15) |
where
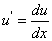 |
(2.16) |
However, this case does not include a type of functional defined by equation (2.14).
The branch of calculus, which deals with the operations performed on functionals, is called as the variational calculus. Some ideas from the variational calculus need to be discussed next.
|