| |
Virtual Work Formulation
Physical interpretation of equation (2.5b) exists if w is interpreted as a virtual displacement. The concept of a virtual displacement can be defined as follows. Note that, because of the forces acting on the bar, it will have some real displacement. Even though it is unknown, a typical real displacement can be represented by a solid curve shown in Fig. 2.2. Now imagine that the bar undergoes some additional small displacement, which is not real but imaginary. Such a displacement is called as virtual displacement and is
denoted by the symbol 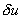 . The dotted line of Fig. 2.2 represents the graph of . The dotted line of Fig. 2.2 represents the graph of 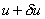 . Thus . Thus 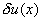 is a function which represents a virtual small change in the value of u(x) at every point of the interval [0, L ]. is a function which represents a virtual small change in the value of u(x) at every point of the interval [0, L ].
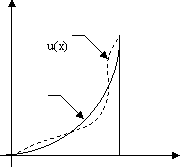
Fig 2.2
We assume that 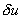 satisfies the same admissibility requirements as that of w . Thus, satisfies the same admissibility requirements as that of w . Thus,
- The virtual displacement must be zero at the boundary where u is zero. Thus, in the present problem,
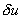 = 0 at x = 0 = 0 at x = 0
- The virtual displacement must be unconstrained at the boundary where the derivative of u is specified. Thus, in the present problem, is unconstrained at x = L
- The virtual displacement
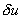 must be smooth enough for an integral of the product of R(x) and to be finite. After the integration by parts, this integral involves the derivative of must be smooth enough for an integral of the product of R(x) and to be finite. After the integration by parts, this integral involves the derivative of 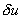 . Thus, in the present problem, . Thus, in the present problem, 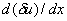 must be finite at every point of the interval [0, L]. must be finite at every point of the interval [0, L].
Thus, the virtual displacement 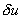 is chosen from the same class of admissible functions from which w is chosen. is chosen from the same class of admissible functions from which w is chosen.
If w is set equal to 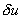 , equation (2.5b) becomes , equation (2.5b) becomes
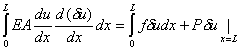 |
(2.6) |
Extension of a bar is a one-dimensional problem. Therefore, u is independent of the other two coordinates y and z . Further, all the stress components other than 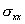 are zero. In particular, are zero. In particular, 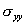 and and 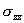 are zero. Thus, are zero. Thus,
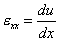 |
(2.7a) |
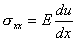 |
(2.7b) |
Further,
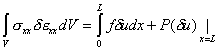 |
(2.9) |
Note that each term in equation (2.9) is an expression of the virtual work. The left side of equation (2.9) represents the virtual work done by the internal forces. The first term on the right side of equation (2.9) represents the virtual work done by the distributed external force f(x). The second term on the right side of the equation (2.9) represents the virtual work done by the point external force P. Together; the right side of equation (2.9) represents the total virtual work of the external forces. What equation (2.9) represents is that: for the residue to be zero (or for u to be a solution of the boundary value problem 2.1a, 2.1b and 2.1c in some sense), the total virtual work must be zero or the virtual work done by the internal forces must be equal to the virtual work done by the external forces.
If the symbol 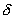 in the expression in the expression 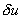 is interpreted as an operator somewhat similar to the differential operator d, equation (2.9) can be transformed to an extremization problem of a quantity called as functional. This gives the second integral form of the boundary value problem. Before it is formulated, it is first necessary to discuss the idea of a functional and its extremum. This is discussed in the next section. is interpreted as an operator somewhat similar to the differential operator d, equation (2.9) can be transformed to an extremization problem of a quantity called as functional. This gives the second integral form of the boundary value problem. Before it is formulated, it is first necessary to discuss the idea of a functional and its extremum. This is discussed in the next section.
|