Weak or Weighted Residual Formulation
Consider a function u ( x ), defined over the interval [0, L ], which satisfies both the boundary conditions (2.1b) and (2.1c) but otherwise arbitrary. In general, such a function will not satisfy the differential equation (2.1a). It means, when u ( x ) is substituted in the left hand side of equation (2.1a), it will not be equal to f ( x ). In this case, the difference is called as residue or error and is denoted by R ( x ). Thus,
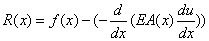 |
(2.2) |
In Weighted Residual Formulation, an approximate solution to the problem (2.1a, 2.1b and 2.1c) is obtained by minimizing the 'weighted' residue or the product of the residue R(x) and certain weight function, denoted by w (x).
The weight function is chosen to be an arbitrary function except that it is required to satisfy the following conditions:
- At the boundary where u is specified, w must be zero. Thus, in the present problem, w = 0 at x = 0.
- At the boundary, where the derivative of u is specified, w must be unconstrained. Thus in the present problem, w is unconstrained at x = L .
- The function w should be smooth enough for the integral of the weighted residue to be finite.
A collection of all the functions, which satisfy the above conditions, is called as a set or class of admissible functions. Thus, the weight function must belong to the class of admissible functions.
One common way of minimizing the residue R(x) is to set the integral of the product of R(x) and w(x) to zero for any admissible function w(x). Thus, an approximate solution to the problem (1a,1b,1c) is obtained from the following equation:
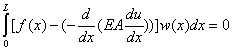 |
(2.3) |
or,
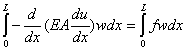 |
(2.4) |
for any w belonging to the class of admissible functions. To relax the smoothness requirements on the choice of the approximate function u(x), the left side of equation (2.4) is usually integrated by parts. This makes the expression symmetric in u and w . By carrying out the integration by parts, equation (2.4) becomes
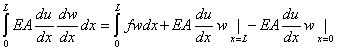 |
(2.5a) |
Since w is zero at x = 0, the last term is zero. Further, u satisfies the boundary condition (2.1c). Then
EA ( 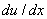 ) at x = L becomes equal to P . With these simplifications, equation (2.5a) becomes: ) at x = L becomes equal to P . With these simplifications, equation (2.5a) becomes:
 |
(2.5b) |
This is called as the weighted residual integral. This is the integral form used in the weighted Residual Formulation. Now the condition 3 of the class of the admissible functions can be made explicit. For all the integrals of equation (2.5b) to be finite, 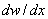 must be finite at every point of the interval (0, L ). It means must be finite at every point of the interval (0, L ). It means 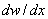 must be piecewise continuous on (0, L ) with only finite discontinuities. must be piecewise continuous on (0, L ) with only finite discontinuities.
Expression (2.5b) is also called as the Weak Formulation of the boundary value problem (2.1a), (2.1b) and (2.1c) because the solution given by the formulation is required to satisfy weaker smoothness conditions compared to that of the solution of the original boundary value problem.
Depending on the choice of w , various special forms of the weighted residual method exist. They are :
(i) Galerkin Method,
(ii) Petrov Galerkin Method and
(iii) Least Square Method.
If the condition of smoothness on w (i.e. the 3rd condition) is relaxed, two more special forms emerge:
(i) Sub-domain Method and
(ii) Collocation Method.
In this lecture, only the Galerkin version of the weighted residual method will be developed. For the details of other version, see the book by Huebener.. |