Bilinear and Quadratic Forms

The two integral formulations discussed above, namely (2.5b) or (2.6) and (2.33) can be expressed conveniently if the following notation is introduced. For any two functions g(x) and h(x) defined over the interval [0, L], we define

• Linear Form :

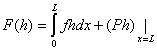(2.45)

• Bilinear Form :

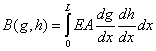(2.46)

• Quadratic Form :

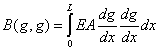(2.47)

Here, L is the length of the bar, f is the distributed force acting on the bar, P is the point force acting on the bar at the end x = L, E is the Young's modulus of the bar and A is the area of the cross-section of the bar.

If u is the axial displacement and w is the weight function, then the integral formulation (2.5b) is obtained by replacing the functions g and h by u and w and equating the expressions (2.45) and (2.46), Thus, the weak or weighted residual formulation is given by

Further, if h is replaced by the virtual displacement 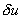rather than by w, then we get the integral form (2.6) corresponding to the virtual work formulation:

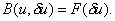(2.49)

If the quadratic form (2.47) is used instead of the bilinear form (2.46), then the integral form (2.33) corresponding to the variational formulation is expressed as

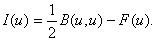(2.50)

Note that the form (2.50) represents an expression, which needs to be extremized to get the solution. On the other hand, the forms (2.48) or (2.49) represent equations, which need to be solved to get the solution.