Expressions for the Element Stiffness Matrix and Element Force Vector
As stated earlier, we use the weighted residual formulation to derive the finite element equations. The corresponding integral form is given by eq. (18.8). Further, we have decided to use the Galerkin scheme. Then, the weight functions are identical to the global basis functions.
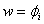 for i = 1,.,2( N +1). for i = 1,.,2( N +1). |
(19.24) |
First, we substitute the above expression for the weight function in the integral form (eq.18.8). Thus, we obtain
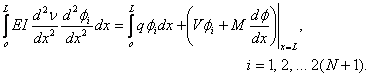 |
(19.25) |
Next, we write the integral form 0 to L as a sum of the integrals over N elements. Thus, we get
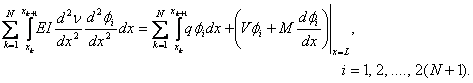 |
(19.26) |
Next, we substitute the finite element approximation (eq. 19.19) in terms of the global basis functions in the above equation. We obtain
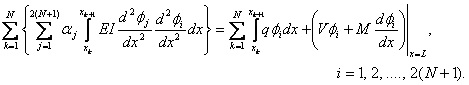 |
(19.27) |
Next, we interchange the sums on the left hand side to get
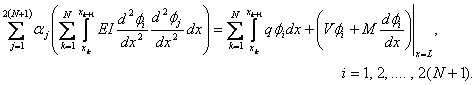 |
(19.28) |
Finally, we define the following quantities :
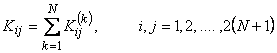 , , |
(19.29) |
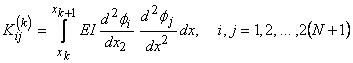 ; ; |
(19.30) |
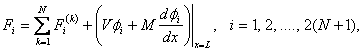 |
(19.31) |
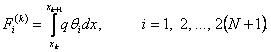 |
(19.32) |
Then, eq. (19.28) becomes
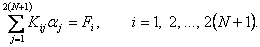 |
(19.33) |
These are the finite element equations. In matrix form, they can be written as
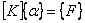 |
(19.34) |
where [ K ] is the global stiffness matrix and 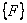 is the global force vector. is the global force vector.
Equations (19.29) and (19.31) show that the global stiffness matrix and the global force vector consist of the contributions 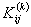 and and 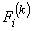 form the elements 1, 2, ., k . The expressions for form the elements 1, 2, ., k . The expressions for 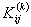 and and 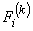 for the k -th element can be simplified as follows. Note that the values of i and j for which for the k -th element can be simplified as follows. Note that the values of i and j for which 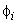 and and 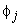 are nonzero over the element k are are nonzero over the element k are
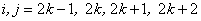 . . |
(19.35) |
Therefore, only 16 elements of 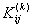 and only 4 elements of and only 4 elements of 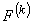 are nonzero. Thus, the matrices are nonzero. Thus, the matrices 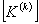 and and 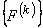 look like : look like :
 |
(19.36) |
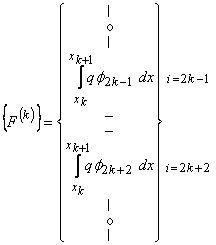 |
(19.37) |
Since only 16 elements of 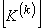 and only 4 elements of and only 4 elements of 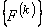 are nonzero, they can be expressed as 4×4 matrix and 4 ×1 vector respectively. Further, we can use the local notation for are nonzero, they can be expressed as 4×4 matrix and 4 ×1 vector respectively. Further, we can use the local notation for 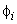 given by eq. (19.22). Then, the nonzero elements of given by eq. (19.22). Then, the nonzero elements of 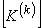 and and 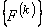 can be expressed as : can be expressed as :
 , , |
(19.38) |
 |
(19.39) |
The 4×4 matrix 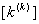 given by eq. (19.38) is called as the element stiffness matrix and the 4 ×1 vector given by eq. (19.38) is called as the element stiffness matrix and the 4 ×1 vector 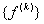 given by eq. (19.39) is called as the element force vector. In index notation, they can be expressed as : given by eq. (19.39) is called as the element force vector. In index notation, they can be expressed as :
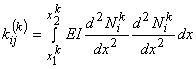 , , |
(19.40) |
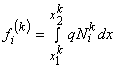 |
(19.41) |
Next, we write these expressions in terms of the natural coordinate 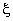 . Using the mapping functions between x and . Using the mapping functions between x and 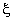 (given by eq.19.14), we first express (given by eq.19.14), we first express 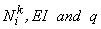 as functions of as functions of 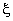 : :
We use the chain rule to evaluate the shape function derivatives. Thus,
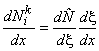 |
(19.43) |
From the mapping function, we get
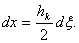 |
(19.44) |
Differentiating eq. (19.43) once more and using the expression (19.44), we get the following expression for the second derivative of 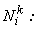
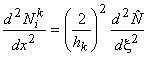 |
(19.45) |
Substituting eqs. (19.42), (19.44) and (19.45) in the expressions (19.40) and (19.41) and changing the limits of integration, we get the following expressions for the integrals of 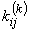 and and 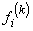 in terms of the natural coordinate in terms of the natural coordinate 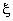 : :
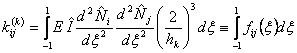 |
(19.46) |
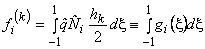 |
(19.47) |
These expressions are integrated using the Gauss quadrature rule (equations 12.38 and 12.39).
To select the number of Gauss points, we make the following assumptions:
-
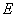 , i.e., the Young's modulus of the beam, is constant. , i.e., the Young's modulus of the beam, is constant.
- The beam has rectangular cross-section. Its width b is constant but the height h decreases linearly (tapered rectangular beam). Then
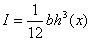 . . |
(19.48) |
Since h ( x ) is a linear polynomial in x , I would be a cubic polynomial in x . Further, since the relation between 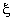 and x is linear, I would be a cubic polynomial in and x is linear, I would be a cubic polynomial in 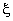 . .
- The distributed force q is a linear function of x . Then,
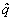 would be a linear polynomial in would be a linear polynomial in 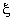 . .
Note that, 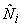 are cubic polynomials in are cubic polynomials in 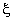 . Then . Then 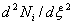 or or 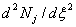 would be linear polynomials in would be linear polynomials in 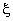 . Now, using the expressions (19.46) and (19.47), the degrees of the integrands . Now, using the expressions (19.46) and (19.47), the degrees of the integrands 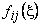 and and 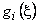 can be estimated as follows. can be estimated as follows.
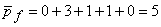 |
|
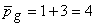 |
(19.49) |
Further,
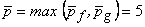 . . |
(19.50) |
Then, the number ( n ) of Gauss points needed for the integration of the expressions (19.46) and (19.47) can be calculated using eq. (12.29) :
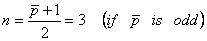 . . |
(19.51) |
|