| |
Expressions for the Assembly of Element Stiffness Matrices and Element Force Vectors
After the evaluation of element stiffness matrix and element force vector for all the elements, we "assemble" these quantities to obtain the global stiffness matrix and the global force vector. As stated in section 6.4, the assembly procedure has the following two steps.
- Expansion of the element stiffness matrix
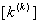 and the element force vector and the element force vector 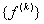 to the full size to obtain the matrices to the full size to obtain the matrices 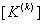 and and 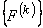 . .
- Addition of the expanded matrices and vectors over all the elements to obtain the global stiffness matrix [K] and the global force vector
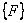 . At this stage, the second term of the expression for . At this stage, the second term of the expression for 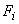 (equation 19.31), which is a contribution from the last node, is also added. (equation 19.31), which is a contribution from the last node, is also added.
The second step is carried out using equations (19.29) and (19.31) and is exactly the same as the second step of the assembly procedure for the bar problem. Now, we discuss the first step. Note that equations (19.38) and (19.39) are the expressions for the element stiffness matrix 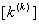 and the element force vector and the element force vector 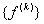 while equations (19.36) and (19.37) are the expressions for their expanded versions while equations (19.36) and (19.37) are the expressions for their expanded versions 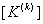 and and 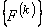 . Further, in the matrix . Further, in the matrix 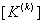 , the first two rows and the first two columns correspond to the first local node of the element. Now, let's see which positions the elements , the first two rows and the first two columns correspond to the first local node of the element. Now, let's see which positions the elements 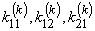 and and 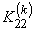 occupy in the expanded matrix occupy in the expanded matrix 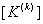 . When we compare equations (19.38) with (19.36), we observe that these 4 elements occupy the positions . When we compare equations (19.38) with (19.36), we observe that these 4 elements occupy the positions 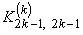 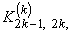 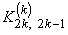 and and 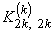 . These 4 positions belong to the row numbers 2k -1 and 2k and the column numbers 2k -1 and 2k of the matrix . These 4 positions belong to the row numbers 2k -1 and 2k and the column numbers 2k -1 and 2k of the matrix 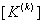 . These 2 rows and 2 columns correspond to the global node k of the beam. This happens because k is the global number of the first local node of the element k . . These 2 rows and 2 columns correspond to the global node k of the beam. This happens because k is the global number of the first local node of the element k .
Thus, the first step involves the following operations :
- Choose the 4 elements of
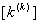 : : 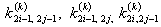 and and 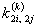 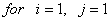 . .
- Find the global numbers of the local nodes i and j of the element k . Let these be r and s respectively.
- Then, these 4 elements of
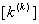 occupy the following positions in the expanded matrix occupy the following positions in the expanded matrix 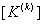 : :
- Repeat the sub-steps (i)-(iii) for other values of i and j .
- The remaining elements of
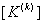 are made zero. are made zero.
The sub-step (ii) can be evaluated using the connectivity matrix [ C ] which relates the local and global node numbering systems. The matrix [ C ] is defined in section 6.4 (for 2-noded element, the expression for [ C ] is given by equation (6.34). Using the definition of [ C ], the sub-step 2 can be expressed mathematically as :
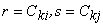 . . |
(19.53)
|
The first step in the assembly of the global force vector 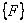 is similar. is similar.
- Choose the 2 elements of
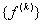 : : 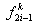 and and 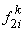 for for 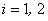 . .
- Find the global number of the local node i . Let it be r . This is found from equation (19.53).
- Then, these 2 elements of
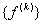 occupy the following positions in the expanded vector occupy the following positions in the expanded vector 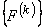 : :
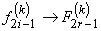 , , |
|
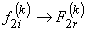 |
(19.54) |
- Repeat the sub-steps (i) - (iii) for other values of i .
- The remaining element of
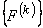 are made zero. are made zero.
Thus, the first step of the assembly procedure is similar to that for the bar problem except for the difference that now a block of 4 elements is considered instead of a single element. This is because, now we have 2 dof per node instead of 1 dof per node of the bar problem.
|