...Contd from the Previous slide...
Now, we define the following functions, called as the shape functions .
These functions are the same as the cubic Hermitian interpolation polynomials . Therefore, these shape functions are called as the Hermitian shape functions . In terms of the shape functions, the approximation (19.9) becomes
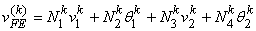 . . |
(19.11) |
Note that the second shape function 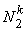 corresponds to the second degree of freedom at the first node corresponds to the second degree of freedom at the first node 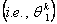 and not the first degree of freedom at the second node and not the first degree of freedom at the second node 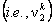 . Thus, the odd shape functions . Thus, the odd shape functions 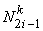 correspond to the first degree of freedom (i.e., the deflection) at the local node i ; whereas the even shape functions correspond to the first degree of freedom (i.e., the deflection) at the local node i ; whereas the even shape functions 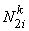 correspond to the second degree of freedom (i.e., the rotation or slope) at the local node i . correspond to the second degree of freedom (i.e., the rotation or slope) at the local node i .
For the purpose of numerical integration, these shape functions need to be expressed in terms of the natural coordinate 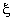 (of the master element). As before, we use the linear mapping function (eq. 11.1) to map a typical element onto the master element (Fig. 19.3). (of the master element). As before, we use the linear mapping function (eq. 11.1) to map a typical element onto the master element (Fig. 19.3).

Figure 19.3 Mapping between a Typical Physical Element k and the Master Element
Thus, the mapping function is
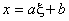 . . |
(19.12) |
The constants a and b are determined from the conditions that the end points 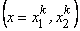 of the physical element map onto the end points of the physical element map onto the end points 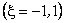 of the master element. Then, we get of the master element. Then, we get
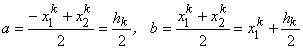 |
(19.13) |
Substituting these expressions in eq. (19.12) and rearranging the terms, we get
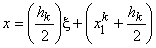 |
(19.14) |
or
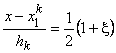 . . |
(19.15) |
Substituting the above mapping function (eq. 19.15) in eq. (19.10), we get the following expressions for the shape functions in terms of 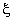 : :
These shape functions are shown in Fig. 19.4.
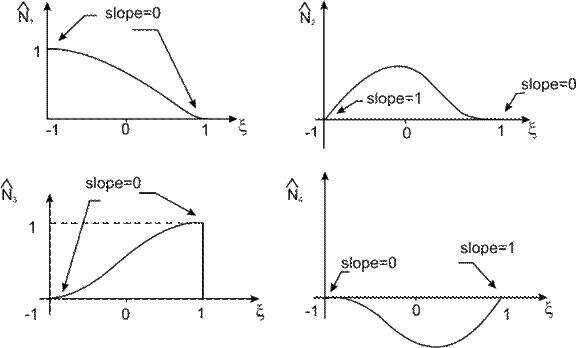
Figure 19.4 Variation of Shape Functions with the Natural Coordinate
From the expressions (19.10), we get the following properties of the shape functions :
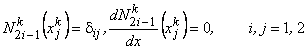 , , |
|
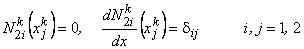 . . |
(19.17) |
These properties are consistent with the variations of the shape functions shown in Fig. 19.4.
Equations (19.10) are the expressions of the simplest Hermitian shape functions. One can develop higher order Hermitian shape functions by considering elements with number of nodes three or more, with degrees of freedom per node being two.
When we use cubic Hermitian shape functions, the global basis functions for the two-element mesh (N=2) would be as shown in Fig. 19.5.
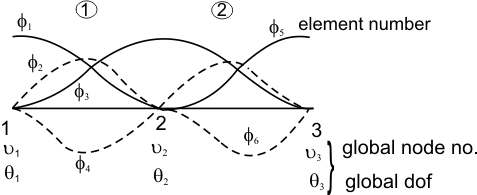
Figure 19.5 Global Basis Functions for Two-Element Mesh (N=2)
For the mesh shown in Fig. 19.5, the finite element approximation in global notation becomes
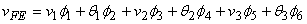 . . |
(19.18) |
Using a single notation for the dof, namely 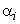 the above expression can be written as the above expression can be written as
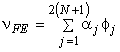 |
(19.19) |
where
 for for 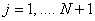 . . |
(19.20) |
From eq. (19.19), one can extract the approximation for k -th element, in global notation, as
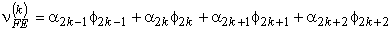 |
(19.21) |
Comparing this approximation with eq. (19.11), we get
and
|

