Shape Functions for the Beam Problem
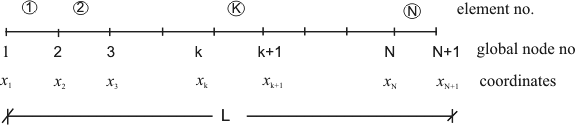
Figure 19.1 Typical Mesh for the Beam Problem
Since, it is a one-dimensional problem, the domain is identical to the interval of length L . Figure 19.1 shows a typical finite element mesh consisting of 2-noded elements. The figure also shows the element numbering scheme, global node numbering scheme and global notation for the nodal coordinates. Figure 19.2 shows a typical element along with the local node numbering scheme, local notation for nodal coordinates and element degrees of freedom.

Figure 19.2 Typical Element
As stated earlier, we need minimum two degrees of freedom (i.e., the primary variable and its first derivative per node to ensure the -continuity of the approximation. The local notation for these degrees of freedom is : and . Since there are 4 degrees of freedom per element, we need 4 linearly independent basis functions. We choose the first four polynomial functions as the basis functions. Then the finite element approximation for k -th element becomes :
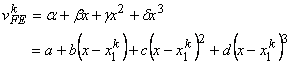 |
(19.1) |
where 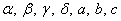 and and 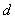 are unknown coefficients. We denote the element length as are unknown coefficients. We denote the element length as 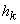 . Thus, we get . Thus, we get
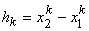 |
(19.2) |
To express the unknown coefficients a , b , c and d in terms of the element degrees of freedom, we evaluate v at the two nodes 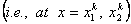 . Thus, we get . Thus, we get
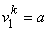 , , |
(19.3) |
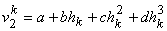 |
(19.4) |
We also evaluate the first derivative :
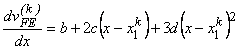 |
(19.5) |
at the two nodes 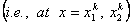 . Thus, we get . Thus, we get
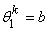 , , |
(19.6) |
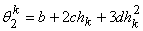 . . |
(19.7) |
Solving these four equations (eqs. (19.3), (19.4), (19.6) and (19.7)), we get the following expressions for a , b , c and d in terms of the degrees of freedom.
Substituting the above expressions in the approximation (eq. 19.1) and rearranging the terms, we get
Contd in the next slide...
|