Variation of Error Norm with Order of Approximation and Mesh Size
For testing the variation of the error norm with the order of approximation ( p ) and the uniform mesh size ( h ), we choose the same problem as that of the last section (Figures 17.2(a) and 17.2(b)) . The error norm 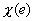 is defined by eqs. (10.1)-(10.2) : is defined by eqs. (10.1)-(10.2) :
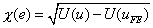 |
(17.8) |
where 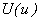 and and 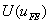 are given by eqs. (17.5)-(17.6). We have shown in Lecture 10 that the variation of are given by eqs. (17.5)-(17.6). We have shown in Lecture 10 that the variation of 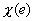 with p and h is given by eq. (10.13) : with p and h is given by eq. (10.13) :
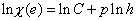 |
(17.9) |
where C is a constant.
We first choose a uniform mesh of size h with p = 1. Then, we calculate the error norm using eqs. (17.5), (17.6) and (17.8). Then, we refine the mesh by decreasing h . We do this for several discrete decreasing values of h and calculate the associated error norm. We repeat these calculations for p = 2 and p = 3. Then, we plot the variation of 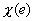 with h for p = 1,2,3. This plot should be similar to Fig. 10.1, i.e., it should appear as shown in Fig. 17.3. with h for p = 1,2,3. This plot should be similar to Fig. 10.1, i.e., it should appear as shown in Fig. 17.3.
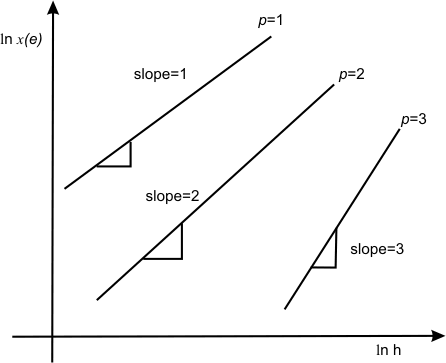
Figure 17.3 Variation of Error Norm with Mesh Size and Order of Approximation
|