Upper Bound and Mesh Convergence
For testing the upper bound and mesh convergence of FE solution, we select the following 2 problems shown in Figures 17.2(a) and 17.2(b).
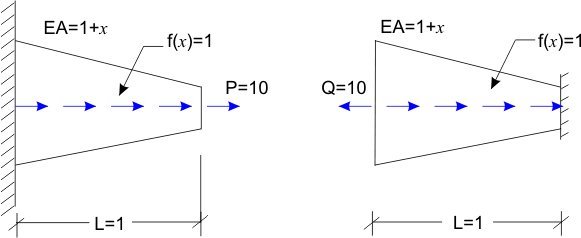
Figure 17.2 Problems for Upper Bound and Mesh Convergence
The exact solutions of the above problems are given by :
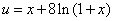 , for problem (a), , for problem (a), |
|
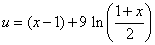 , for problem (b) , for problem (b) |
(17.4) |
Note that these solutions are not polynomials in x . We calculate the strain energy of the exact solution using eq. (9.25) :
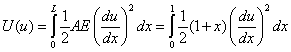 |
(17.5) |
Now we choose a uniform mesh of N elements with some value for N . Further, we choose the order of approximation p as one. Then, we obtain the FE solution 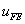 by using the FE code. We calculate strain energy of the FE solution using eq. (10.10) : by using the FE code. We calculate strain energy of the FE solution using eq. (10.10) :
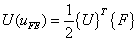 |
(17.6) |
where { F } is the global force vector and { U } is the vector containing nodal values of the displacement. We compare 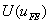 with with 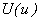 to test whether the inequality to test whether the inequality
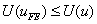 |
(17.7) |
is satisfied or not. Next, we obtain 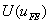 by keeping the value of p fixed but by refining the mesh, i.e., by increasing N . Then also the inequality (17.7) should be satisfied. Further, as N is increased, by keeping the value of p fixed but by refining the mesh, i.e., by increasing N . Then also the inequality (17.7) should be satisfied. Further, as N is increased, 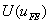 should approach should approach 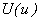 monotonically. If we choose some other value of p instead of one, then also the inequality (17.7) and the monotonic convergence of monotonically. If we choose some other value of p instead of one, then also the inequality (17.7) and the monotonic convergence of 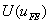 to to 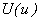 from below should be observed. from below should be observed.
|