| |
Quadratic Approximation ( p = 2 )
Shape functions 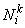 , i = 1,2,3 for this case are given by (equation 8.6): , i = 1,2,3 for this case are given by (equation 8.6):
Since p = 2, the mapping function (equation 11.7) becomes:
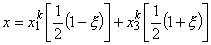 |
(11.19) |
Note that the nodes 1 and 3 are at the end points of the element. Let us choose node 2 at the midpoint. Then
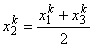 |
(11.20) |
One can obtain the shape functions in terms of x by substituting equations (11.19-11.20) into the expressions (11.16-11.18). But this procedure is cumbersome. Therefore, we follow an alternate procedure which is more convenient. This procedure involves the use of expression (11.1) for the mapping function. It is described in the next paragraph.
Let
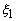 , ,
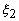 and and
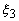 be the natural coordinates of the nodes 1, 2 and 3 respectively. Note that node 1 is at the left end ( be the natural coordinates of the nodes 1, 2 and 3 respectively. Note that node 1 is at the left end (
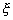 = -1) and the node 3 is at the right end ( = -1) and the node 3 is at the right end (
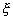 = 1). Further, the node 2 is at the center ( = 1). Further, the node 2 is at the center (
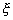 = 0). Thus, = 0). Thus,
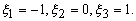 |
(11.21) |
The relation between the physical coordinate 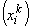 of the node i and its natural coordinate ( of the node i and its natural coordinate (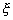 i ) can be obtained from equation (11.1) as follows: i ) can be obtained from equation (11.1) as follows:
Therefore, combining equations (11.1) and (11.22), we get
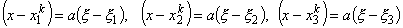 |
(11.23) |
Further, from equation (11.22), we get
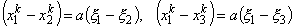 , , |
(11.24) |
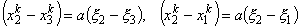 , , |
(11.25) |
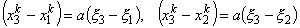 , , |
(11.26) |
Substituting equations (11.23 -11.26) in expressions (11.16 -11.18) and canceling out the factor a2 from the numerator and denominator, we get
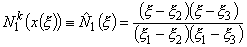 , , |
(11.27) |
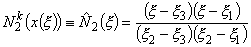 , , |
(11.28) |
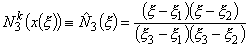 , , |
(11.29) |
Using the values of 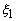 , , 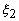 and and 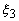 (equation 11.21), the above expressions can be simplified to (equation 11.21), the above expressions can be simplified to
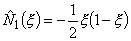 , , |
(11.30) |
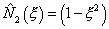 , , |
(11.31) |
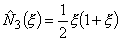 , , |
(11.32) |
These shape functions are shown in Fig 11.3. The quantity hk denotes the element length 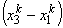 . The nodes are marked by the symbol x . . The nodes are marked by the symbol x .
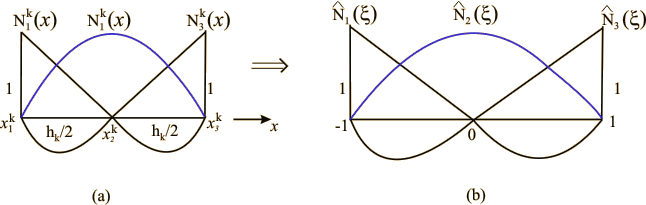
Fig. 11.3 Shape functions for quadratic approximation (p = 2)
(a) For physical element k (b) For master element
|