Approximation of Order p
Shape functions 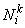 , i =1,2,., p+1 for this case are given by (equation 8.8): , i =1,2,., p+1 for this case are given by (equation 8.8):
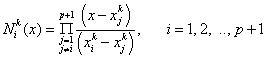 |
(11.33) |
If we use equation (11.7) as the expression of mapping function to represent these shape functions in terms of the natural coordinate 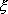 , Then the corresponding procedure is quite cumbersome. Therefore, we follow a simpler procedure which involves the use of expression (11.1) for the mapping function. This procedure is described in the next paragraph. , Then the corresponding procedure is quite cumbersome. Therefore, we follow a simpler procedure which involves the use of expression (11.1) for the mapping function. This procedure is described in the next paragraph.

Fig. 11.4 Nodal coordinates for approximation of order p
(a) For physical element k (b) For master element
Figure 11.4 shows the nodal coordinates for the physical element k and the master element. We choose the nodes to be equidistant. There are p+1 nodes . Thus, the nodes divide the element length into p equal intervals. For the physical element k , the x -coordinates of the nodes can be expressed as
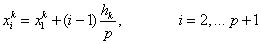 |
(11.34) |
where hk is the element length. For the master element, the element length is 2. Further since the node 1 is at the left end, 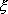 -coordinate of node 1 ( -coordinate of node 1 ( 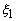 ) is 1. Therefore, the ) is 1. Therefore, the 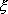 -coordinate of the nodes can be expressed as -coordinate of the nodes can be expressed as
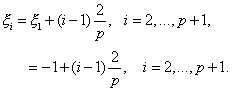 |
(11.35) |
Note that the relation between the physical coordinate 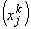 of node j and its natural coordinate of node j and its natural coordinate  can be obtained from equation (11.1) as follows: can be obtained from equation (11.1) as follows:
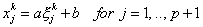 |
(11.36) |
Then, subtracting equation (11.36) from equation (11.1) we get
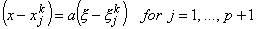 |
(11.37) |
Similar to expression (11.36), we can write
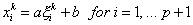 |
(11.38) |
Subtracting equation (11.36) from equation (11.38), we get
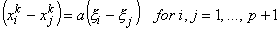 |
(11.39) |
Substituting equations (11.37) and (11.39) into the expression (11.33) and canceling out the factor a p both from the numerator and denominator, we get the following expression for the shape functions:
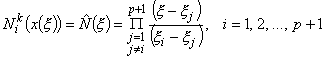 |
(11.40) |
Here, 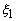 = -1 and the remaining nodal coordinates are given by the expression (11.35). = -1 and the remaining nodal coordinates are given by the expression (11.35).
Note that, we get expressions (11.14 - 11.15) for the linear shape functions when we substitute p = 1, 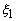 = -1 and = -1 and 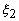 = +1 in equation (11.40). Similarly, we get the expressions (11.30 -11.32) for the quadratic shape functions if we substitute p = 2, = +1 in equation (11.40). Similarly, we get the expressions (11.30 -11.32) for the quadratic shape functions if we substitute p = 2, 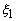 = -1, = -1, 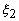 = 0, = 0, 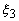 = + 1 in equation (11.40). = + 1 in equation (11.40).
|