Linear Approximation (p = 1) :

Shape functions 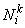, i = 1,2 for the linear approximation are given by (equations 6.1 and 6.2) :

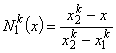
	(11.9)
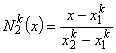	(11.10)

Since p = 1, the mapping function (equation 11.7) becomes:

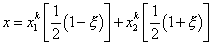(11.11)

One can obtain the shape functions in terms of 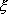by using either the expression (11.1) or expression (11.11) for the mapping function. For the present case of linear approximation, we use expression (11.11). For the next case, we shall show how to use the expression (11.1). Using expression (11.11), we get

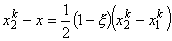
	(11.12)
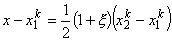	(11.13)

Substituting these expressions in equations (11.9-11.10) and canceling out the factor 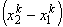from both the numerator and denominator, we get the following expressions for the shape functions:

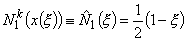	(11.14)
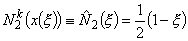	(11.15)

The shape functions are shown in Fig. 11.2. The quantity h k denotes the element length 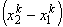. The nodes are marked by the symbol x.

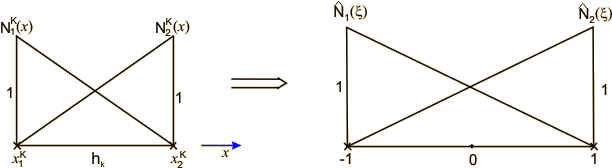
Fig. 11.2   Shape functions for linear approximation (p = 1)
(a) for physical element k        (b)  For master element