Error Estimate
It can be shown that (Reference)
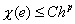 |
(10.11) |
where C is a constant, p is the order of approximation and h is the (uniform) mesh size, given by
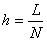 |
(10.12) |
Here, L is the length of the domain and N is the number of elements. Inequality (10.11) shows that as the number of elements ( N ) increases or equivalently the mesh size ( h ) decreases, the norm of the error function decreases, that is, the difference between the exact solution and the FE solution decreases. Thus, FE solution tends to the exact solution when 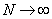 or or 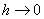 . The exponent of h in inequality (10.11) denotes the rate of convergence. . The exponent of h in inequality (10.11) denotes the rate of convergence.
Taking the natural logarithm of both sides of the inequality (10.11) and using only the equal sign , we get
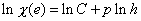 |
(10.13) |
Variation of 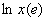 with with 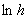 for various values of p is shown in Fig. 10.1. for various values of p is shown in Fig. 10.1.
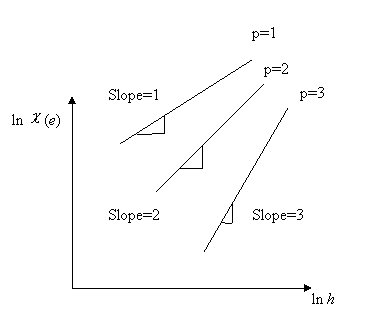
Figure 10.1 Variation of error norm with mesh size
|