Error Norm
The norm of the error function e , denoted by 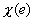 , is defined as square root of the strain energy of the error function U( e ). Thus, , is defined as square root of the strain energy of the error function U( e ). Thus,
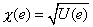 |
(10.1) |
In the last lecture, we showed that
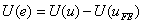 |
(10.2) |
where u is the exact solution and 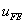 is the finite element solution. The expressions for the strain energies is the finite element solution. The expressions for the strain energies 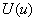 and and 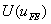 are given by are given by
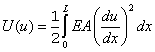 |
(10.3) |
and
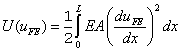 |
(10.4) |
Now we shall express 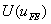 in terms of the global stiffness matrix [ K ]. First, substitute the FE approximation in terms of the global stiffness matrix [ K ]. First, substitute the FE approximation
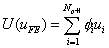 |
(10.5) |
into equation (10.4). Here, N is the number of elements, p is the order of approximation, 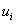 are the nodal values of the primary variable and are the nodal values of the primary variable and 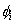 are the basis functions. Thus, we get are the basis functions. Thus, we get
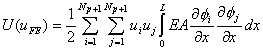 |
(10.6) |
Using the definition of the Kij (equation 3.13), this can be written as
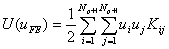 |
(10.7) |
In matrix form, this can be expressed as
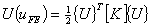 |
(10.8) |
where { U } is the global displacement vector. Using the finite element equation
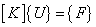 |
(10.9) |
the above equation can be expressed as
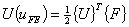 |
(10.10) |
The global stiffness matrix [K], besides being a function of the material property E and the geometric property A ,also depends on mesh size h . Equation (6.58) shows that, when EA is constant, [K] is inversely proportional to h for the case of linear approximation. The dependence of [K] for other approximations can be worked out similarly. Thus, using equations (10.2), (10.3) and (10.8), the error norm 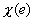 can be approximated as a function of h. can be approximated as a function of h.
|