Let us define the control-law as
 |
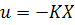(25.3) |
where, the control-gains are represented in a matrix-form. For a single input system, u becomes scalar and consequently K may be expressed as
 |
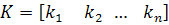(25.4) |
Substituting Eqn 25.3 into the state equation 24.1, one can get the state-space equation as
 |
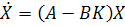(25.5) |
 |
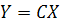The characteristic equation corresponding to the closed-loop plant may be expanded as
 |
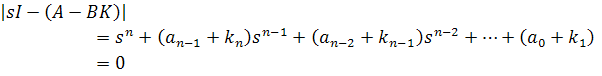(25.6) |
When the desired roots of the closed-loop system
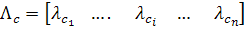 (the subscript c denotes roots corresponding to Canonical form) are known, the desired characteristic equation may be obtained as
 |
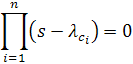(25.7) |
or  |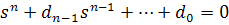
By comparing the coefficients of the polynomials of eqns. (25.6) and (25.7) one can get the elements of control gain vector KC as
 |
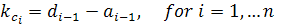(25.8) |
|
