If the system is not in control canonical form, one needs to find the proper transformation matrix T to convert the system into canonical form. If x is the state vector corresponding to non-canonical form along with the corresponding state-space parameters A , B and C and z is the state vector in canonical form along with system parameters given by A_c , B_c and C_c , then, considering T to be the transformation matrix between the two linear systems such that

	(25.9)

After obtaining the controllability matrix related to the non-canonical form with the help of eqn. (25.1), one can obtain the controllability matrix corresponding to the canonical form as

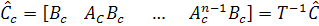(25.10)

Eqn. (25.10) can be used to obtain the transformation matrix as .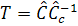

After converting the system into canonical form one can use the eqns. (25.4) to (25.8) to obtain the control gains. The control gain vector K_C thus obtained could be reconverted to initial non-canonical form by using the following relationship

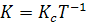(25.11)