The Root Locus method
The root locus method is used to study the change in the pole-location of a closed-loop system in the s-plane with respect to the change in the control-gain. A simple closed loop system is described as follows:
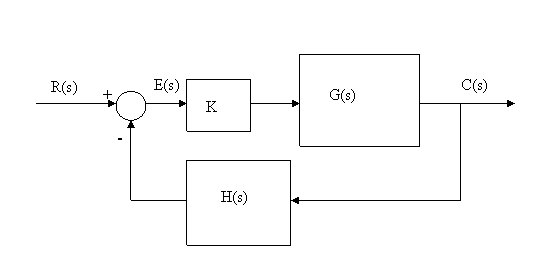
Figure 23.5: A simple closed loop system
Following the block-diagram, the error E(s) is
| E(s) = R(s) – H(s) C(s) |
(23.9) |
Again
| C(s) = K G(s) E(s) = K G(s) [R(s) – H(s) C(s)] |
(23.10) |
Hence,
| C(s)/R(s) = K G(s) /[1+K G(s) H(s)] |
(23.11) |
Equation (24.11) is known as the closed-loop transfer function for a negative feed-back system. The characteristic equation corresponding to a unity feedback (H(s) =1) for the above system could be written as
The above equation could be expressed in terms of magnitude and phase as follows:
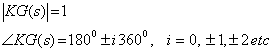 |
(23.13) |
Using the phase relationship of the above equation, one can plot the locus of the roots of the characteristic equation as K varies from 0 to infinity.
The following are the basic rules used for plotting the root-locus corresponding to a transfer function having n open-loop poles and m open-loop zeros.
- The n branches of root-locus start at the n open-loop poles and out of them m branches end at the m open-loop zeros, while the n-m branches end at infinity.
- On the real axis, the root-loci exist on the left side of odd number of poles and zeros.
- The root locus is symmetric about the real axis.
- The asymptotes of root-locus at infinity have the following real-axis intercept σ and angle θ:
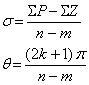
where, P and Zs are finite poles and zeros already defined by Eqn.23.5.
- The angle of arrival and departure from the poles and zeros are calculated by choosing a point very close to such desired poles and zeros. Now, using a simple graphical technique, vectors are drawn to the desired pole/zero from all the other poles and zeros. Adding the angles of the zeros and subtracting that of the poles the net angle is obtained at the point as θnet . Subtracting this angle from 1800 would yield the angle of departure/arrival of the root-locus.
- The root-locus crosses the imaginary axis at the points where the angle of G(s)H(s) becomes equal to (2k+1)1800 .
|