Response of First and Second Order Systems

A first order system is denoted by a system having a first order denominator-polynomial.

The system may be represented in two ways

            in a block-diagram form

           by showing the poles and zeroes of the transfer function in a plot known as s-plane.

The figures below show the two representations: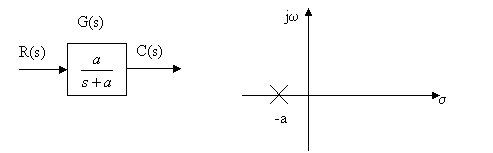

Here, the symbol ‘x' denotes the pole location. R(s) denotes the input signal and C(s) the output or response of the system. The first order system is symbolically represented as G(s); ‘a' is also known as the time constant of the system. It may be noted that for a stable system the poles are always located at the left-half region of σ , jω plane.

The transfer function G(s) for a second order system is denoted as

Here, ω_n denotes the frequency of the system and ς the damping ratio. For an under-damped system, the roots of the denominator polynomial would be a pair of complex conjugate points in the s-plane and the corresponding response of such a system to a step input is shown in the figure below.

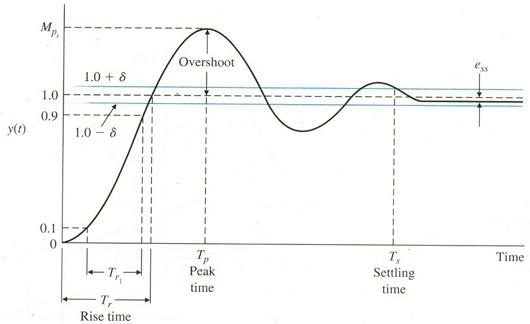
Figure 23.4: Time response of a second order system

There are four major specifications that define the response of a second order system.

The swiftness of the response is measured by the rise time (T_r ), which is defined as the time required reaching 90% of the reference input.

The closeness of the response signal to the reference is measured in terms of % overshoot ( PO ) such that

PO = ((M_p – final value)/final value)*100

The time taken to reach the maximum response is denoted by Peak Time (T_p ) . The % overshoot is measured at the same location. Finally, the Settling Time (T_s ) is defined as the time required for the system to settle within a certain percentage of the reference input (±δ ).

For a second order system, the above four specifications could be defined in terms of natural frequency and damping factor of the system as:

(23.8)