Review of Laplace Transformation
Laplace Transformation is a very useful tool for Designing Controller in the Frequency-Domain. This transformation helps to transform differential equation into the form of algebraic equations which is easier to manipulate.
A time-domain signal f(t) which may represent a forcing function or the response of a system may be transformed into frequency domain by using the following transformation:
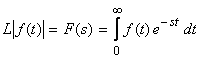 |
(23.1)) |
Where s = σ + jω , is a complex variable.
Example:
f(t) = A e -pt u(t)
|
|
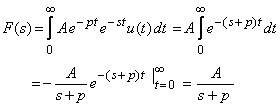 |
Table 23.1: Some of the frequently required Laplace transformations:
S.No. |
f(t), t = 0 |
F(s) |
1 |
δ (t) |
1 |
2 |
u(t) |
1/s |
3 |
t |
1/s2 |
4 |
t2 |
L 2/s3 |
5 |
e−at |
1/(s+a) |
6 |
sin at |
a/(s2 + a2 ) |
7 |
cos at |
s/(s2 + a2 ) |
8 |
(1-at) e−at |
s/(s+a)2 |
Applying the same principle on a differential equation one can obtained an algebraic equation. Consider a second order system as
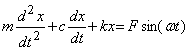 |
(23.2) |
Applying Laplace transformation and assuming zero initial condition the above equation could be transformed as
Denoting the right hand side of the above equation as 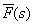 , one can express the ratio of frequency-domain response X(s) and , one can express the ratio of frequency-domain response X(s) and 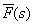 as as
T(s) is also known as transfer function of the system.
In a block diagram form, this can be represented as

The response of a system in time domain could be obtained by carrying out Inverse Laplace Transformation of the transfer function. The inverse Laplace Transform is written as
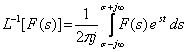 |
(23.3) |
However, this relationship is seldom used. If F(s) is rational, one commonly uses the method of partial fraction expansion. Consider a rational function F(s) expressed as:
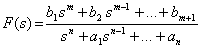 |
(23.4) |
Factoring the numerator and denominator polynomials one can also write
 |
(23.5) |
Corresponding to the numerator polynomial, zis are referred as the zeros of the transfer function while the roots of the numerator polynomial pi's are known as the poles of the transfer function.
Now, the transfer function F(s) may be expressed as
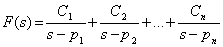 |
(23.6) |
where,
Finally, the response of the system may be expressed as
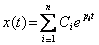 |
(23.7) |
|