VALIDATION OF RECONSTRUCTION PROCEDURE WITH SIMULATED DATA
The goal of the present work is to obtain concentration distribution on selected planes above the crystal growing from its aqueous solution from the schlieren images. These images require to be extrapolated to fill the width of the beaker. The extrapolation step combined with the convolution back-projection algorithm is first validated against simulated data. The physical problem considered is buoyancy-driven convection in a differentially heated circular fluid layer with upper and lower walls maintained at specified temperatures. The side wall that is circular is thermally insulated. The fluid considered is air and the Rayleigh number based on the height of the fluid layer is set at 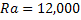 . The temperature distribution in the fluid layer has been obtained by numerically solving the governing equations of flow and energy transport on a fine grid. For definiteness, the thermal field is taken to be axisymmetric; accordingly the isotherms on individual planes of the fluid layer are circular. . The temperature distribution in the fluid layer has been obtained by numerically solving the governing equations of flow and energy transport on a fine grid. For definiteness, the thermal field is taken to be axisymmetric; accordingly the isotherms on individual planes of the fluid layer are circular.
With the solution for temperature determined numerically, the projection of the thermal field is obtained by path integration. The accuracy of reconstruction with partial data has been examined in the present study against the available numerical solution.
Errors have been reported in the present section on three grids, namely 64 X 64, 128 X 128 and 256 X 256. Here, the first number represents the number of view angles along which projections have been recorded, and the second indicates the number of rays for each view. The definitions of errors considered are:
|
absolute maximum temperature difference |
Here 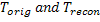 are the original and reconstructed temperature fields respectively and are the original and reconstructed temperature fields respectively and 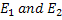 arises from the fact that the former highlights large isolated errors, while the latter reveals trends that are applicable for the entire cross-section. arises from the fact that the former highlights large isolated errors, while the latter reveals trends that are applicable for the entire cross-section.
|