In the definitions given in the previous slide for quantities such as 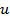 and and 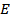 the signal the signal 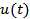 is available in digital form and stored in a computer. Many of these integrals can instead be evaluated in terms of the probability density function is available in digital form and stored in a computer. Many of these integrals can instead be evaluated in terms of the probability density function 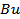 of the signal of the signal 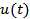 . The advantages of this approach are: . The advantages of this approach are:
1. 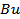 can be determined using hardware (instruments) and, can be determined using hardware (instruments) and,
2. 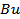 is a usually a smooth function of its argument and hence integrals involving is a usually a smooth function of its argument and hence integrals involving 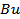 can be accurately calculated by high order numerical integration formulas. can be accurately calculated by high order numerical integration formulas.
However, the difficulty of having a long enough signal for 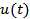 is now transferred to waiting for a long enough time to determine is now transferred to waiting for a long enough time to determine 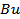 . The accuracy with which . The accuracy with which 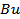 is measured depends on the choice of the window is measured depends on the choice of the window 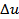 and total time and total time 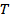 . .
In general, for small values 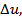 a large value of time a large value of time 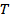 is required for satisfactory convergence of the limit process arising in the definition of is required for satisfactory convergence of the limit process arising in the definition of 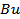 . In terms of . In terms of 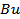 the mean and RMS values are defined as follows: the mean and RMS values are defined as follows:
For signals that do not have a zero mean
The 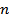 th order moment of a signal with a zero mean is defined as th order moment of a signal with a zero mean is defined as
|