A Gaussian signal is one whose probability density function has a Gaussian profile. Such signals have a finite range of values of time lag over which the autocorrelation 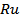 is non-zero. Additionally, the power spectrum, interpreted as the harmonically decomposed kinetic energy, is spread over a range of frequencies. The central limit theorem of probability theory is worth recalling in this connection. This theorem states that a large number of identically distributed independent variables will together have a Gaussian probability density function regardless of the shape of the density of the variables themselves. Signals in homogeneous, stationary turbulent flow that exhibit equilibrium between energy production and dissipation are known to exhibit a Gaussain probability density function . Hence deviation from Gaussain behaviour can be used as a measure of deviation from equilibrium itself. is non-zero. Additionally, the power spectrum, interpreted as the harmonically decomposed kinetic energy, is spread over a range of frequencies. The central limit theorem of probability theory is worth recalling in this connection. This theorem states that a large number of identically distributed independent variables will together have a Gaussian probability density function regardless of the shape of the density of the variables themselves. Signals in homogeneous, stationary turbulent flow that exhibit equilibrium between energy production and dissipation are known to exhibit a Gaussain probability density function . Hence deviation from Gaussain behaviour can be used as a measure of deviation from equilibrium itself.
The shape of a Gaussian PDF for a zero-mean signal 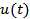 is given by the formula is given by the formula
and is sketched in Figure 1.12. Here, 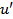 is the RMS value of is the RMS value of 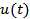
Figure 1.12: An Example of Gaussian PDF. |
|