Contd...
Here 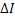 is the change in illumination on the screen due to the beam displacement from its original path and is the change in illumination on the screen due to the beam displacement from its original path and 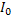 is the original intensity distribution. Equation 22 implies that the shadowgraph is sensitive to changes in the second derivative of the refractive index along the line of sight of the of the light beam in the fluid medium. Integration of the Poisson equation (22) can be performed by a numerical technique, say the method of finite differences. is the original intensity distribution. Equation 22 implies that the shadowgraph is sensitive to changes in the second derivative of the refractive index along the line of sight of the of the light beam in the fluid medium. Integration of the Poisson equation (22) can be performed by a numerical technique, say the method of finite differences.
From Equation 22 it is evident that the shadowgraph is not a suitable method for quantitative measurement of the fluid density, since such an evaluation requires one to perform a double integration of the data. However, owing to its simplicity the shadowgraph is a convenient method for obtaining a quick survey of flow fields with varying fluid density. When the approximations involved in Equation 22 do not apply, shadowgraph can be used for flow visualization alone.
The present lecture has a discussion on how shadowgraph images can be analyzed to retrieve information on the concentration field.
Shadowgraphy
It employs an expanded and collimated beam of laser light. The light beam traverses the field of disturbance, an aqueous solution of KDP in the present application. If the disturbance is a field of varying refractive index, the individual light rays passing through the field are refracted and bent out of their original path. This causes a spatial modulation of the light intensity distribution. The resulting pattern is a shadow of the refractive-index field in the region of the disturbance.
Governing equation and Approximations
Consider a medium with refractive index 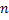 that depends on all the three space coordinates, namely that depends on all the three space coordinates, namely 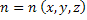 . We are interested in tracing the path of light rays as they pass through this medium. Starting with the knowledge of the angle and the point of incidence of the ray at the entrance plane, we would like to know the location of the exit point on the exit window, and the curvature of the emergent ray. . We are interested in tracing the path of light rays as they pass through this medium. Starting with the knowledge of the angle and the point of incidence of the ray at the entrance plane, we would like to know the location of the exit point on the exit window, and the curvature of the emergent ray.
Let the ray be incident at point 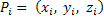 and the exit point be and the exit point be 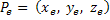 . According to Fermat's principle the optical path length traversed by the light beam between these two points has to be an extremum. If the geometric path length is . According to Fermat's principle the optical path length traversed by the light beam between these two points has to be an extremum. If the geometric path length is 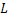 , then the optical path length is given by the product of the geometric path length with the refractive index of the medium. Thus , then the optical path length is given by the product of the geometric path length with the refractive index of the medium. Thus
|