Parameterizing the light path by 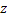 , the condition (Equation 23) can be represented by two functions , the condition (Equation 23) can be represented by two functions 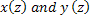 , and the equation can be written as , and the equation can be written as
where the primes denote differentiation with respect to 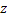 . Application of the variational principle to the above equation yields two coupled Euler-Lagrange equations, that can be written in the form of the following differential equations for . Application of the variational principle to the above equation yields two coupled Euler-Lagrange equations, that can be written in the form of the following differential equations for 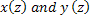 : :
The four constants of integration required to solve these equations comes from the boundary conditions at the entry plane of the chamber. These are the co-ordinates 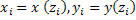 of the entry point of the entry point 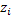 and the local derivatives and the local derivatives 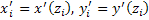 . The solution of the above equation yields the two orthogonal components of the deflection of the ray at the exit plane, and also its gradient on exit. . The solution of the above equation yields the two orthogonal components of the deflection of the ray at the exit plane, and also its gradient on exit.
In the experiments performed, the medium has been confined between parallel planes and the illumination is via a parallel beam perpendicular to the entry plane. The length of the growth chamber containing the fluid is D and the screen is at a distance 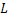 behind the growth chamber. The behind the growth chamber. The 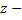 coordinates at entry, exit and on the screen are given by coordinates at entry, exit and on the screen are given by 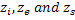 respectively. Since the incident beam is normal to the entrance plane, there is no refraction at the optical window. Hence the derivatives of all the incoming light rays at the entry plane are zero; respectively. Since the incident beam is normal to the entrance plane, there is no refraction at the optical window. Hence the derivatives of all the incoming light rays at the entry plane are zero; 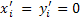 . The displacements . The displacements 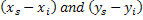 of the light ray on the screen of the light ray on the screen 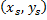 with respect to its entry position with respect to its entry position 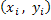 are are
where 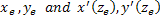 are given by the solutions of previous equations at are given by the solutions of previous equations at 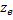 . .
The above formulation can be further simplified with the following assumptions.
|