The above derivation of temperature difference between successive fringes will be modified in the presence of a strong refracting field. In the present context, a strong refracting field will arise when a large transverse temperature gradient is present. The light ray will not travel in a single horizontal plane, and depending on the sign of the temperature gradient, the ray will bend in the vertical plane owing to refraction effects. Refraction, thus will introduce an additional optical path length to the test beam. Refraction effects can be precisely computer and accounted for. The extent of refraction determines the type of the three-dimensional reconstruction algorithm errors was found to be negligible and hence a sequence a sequential plane-by plane reconstruction approach was possible.
An estimate of the increase in path length due to refraction is developed here. Following Goldstein [4], consider the path of the light ray through a test cell (Figure: 4.30) when it is affected by the refraction effects. Let 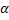 be the bending angle at a location P of the test cell. The optical path length from A to B is given by: be the bending angle at a location P of the test cell. The optical path length from A to B is given by:
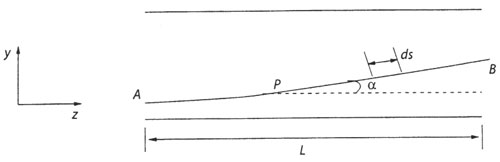
Figure 4.30: Calculation of bending angle of light ray due to refraction effects.
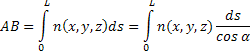
Here 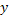 is a coordinate parallel to the gravity vector and is a coordinate parallel to the gravity vector and 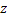 is parallel to the direction of propagation of light. Assuming is parallel to the direction of propagation of light. Assuming 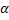 is small, cos is small, cos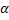 can be expressed as can be expressed as
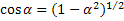
and further using the first two terms of the binomial expansion
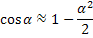
Hence the optical path length is given by
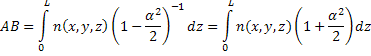
The angle 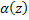 at any location at any location 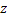 can be calculated as described in next slide. can be calculated as described in next slide.
|