The integral is defined as where is the average value of over the length L of the laser beam through the test cell. This is also the line integral of the function . Hence

(9)

In the infinite fringe setting Equation (9) holds good for all fringes. When is constant for all the rays, Equation (9) implies that is a constant over the fringe and hence each fringe represents a locus of points over which the average of the temperature field along the direction of the ray is a constant; in this sense, fringes are isotherms.

Consider a geometry where the length of the ray through the test cell changes for each ray. The line integral of the function at a location which corresponds to a length can be given in terms of the line integral of the function at some other location corresponding to a ray length of as

(10)

Since the change in path length per fringe shift is a constant, the temperature drop per fringe shift is a also a constant. Defining the function in Equation (9) as the fringe temperature on two successive fringes for same value of L can be given as

where is the wavelength of the laser used. From these two equations, the temperature change per fringe shift can be calculated as

(11)

The interferogram reflects the equation

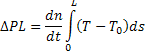
This  shows that the fringe patterns contain information about the line integral of the temperature field. The set of all line integrals (an interferogram, in the present study) defines a projection of the temperature field. The interferograms can be numerically processed so that the left side of the above equation is a known quantity. The mathematical problem now is one of solving the temperature field from its projections. If the original field is three-dimensional, its projection is a field in a dimension reduced by unity, i.e., two for the present case. It is theoretically possible to record a large number of projections of the field at various angles and reconstruct the original temperature function with accuracy. This process of three-dimensional reconstruction from two-dimensional projections, called tomography, is discussed in later sections.