Fundamentals of Fluid Flow Modeling
We have discussed the finite-difference methods with respect to the solution of linear problems such as heat conduction. The problems of fluid mechanics are more complex in character. The governing partial differential equations form a nonlinear system which must be solved for the unknown pressures, densitities, temperature and velocities.
Before entering into the domain of actual flow modeling, we shall discuss some subtle points of fluid flow equations with the help of a model equation.
The model equation should have convective, diffusive and time-dependent terms. Burgers (1948) introduced a simple nonlinear equation which meets the aforesaid requirements (Burger's equation).
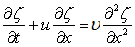 |
(9.11) |
Here, u is the velocity, 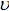 is the coefficient of diffusivity and is the coefficient of diffusivity and 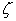 is any property which can be transported and diffused. is any property which can be transported and diffused.
If the viscous term (diffusive term) on the right-hand side is neglected, the remaining equation may be viewed as a simple analog of Euler's equation.
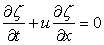 |
(9.12) |
Now we shall see the behavior of Burger's equations for different discretization methods. In particular, we shall study their influence on conservative and transportive property, and artificial viscosity.
|