Let us look at the stability requirement for the second-order wave equation given by
We replace both the spetial and time derivative with central difference scheme (which is second-order accurate)
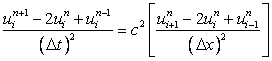 |
(9.1) |
Again assume
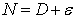 |
(9.2) |
and
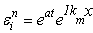 |
(9.3) |
Substituting Eq. (9.3) and (9.2) in (9.1) and dividing both side by 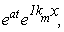 we get we get
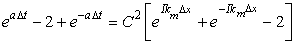 |
(9.4) |
where
C, the Courant number 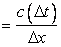 |
(9.5) |
From Eq. (9.4), using trigonometric identities, we get
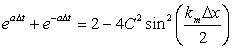 |
(9.6) |
and, the amplification factor
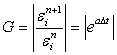 |
(9.7) |
However, from Eq. (9.6) we arrive at
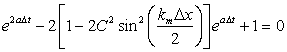 |
(9.8) |
Which is a quadratic equation for 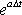 This equation, quite obviously, has two roots, and the product of the roots is equal to +1. Thus, it follows that the magnitude of one of the roots (value of This equation, quite obviously, has two roots, and the product of the roots is equal to +1. Thus, it follows that the magnitude of one of the roots (value of 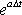 ) must exceed 1 unless both the roots are equal to unity. ) must exceed 1 unless both the roots are equal to unity.
But 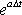 is the magnification factor. If its value exceeds 1, the error will grow exponentially which will lead to an unstable situation. All these possibilities mean that Eq (9.8) should possess complex roots in order to both have the values of is the magnification factor. If its value exceeds 1, the error will grow exponentially which will lead to an unstable situation. All these possibilities mean that Eq (9.8) should possess complex roots in order to both have the values of 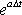 equal to unity. equal to unity.
This implies that the discriminant of Eq. (9.8) should be negative.
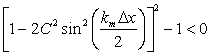 |
(9.9) |
or
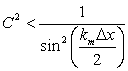 |
(9.10) |
which is always true if 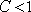 . .
Hence CFL condition 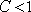 , must again be satisfied for the stability of second-order hyperbolic equations. , must again be satisfied for the stability of second-order hyperbolic equations.
|