In light of the previous discussion, we can say that a finite-difference procedure will be unstable if for that procedure, the solution becomes unbounded, i.e the error grows exponentially as the calculation progresses in the marching direction.

In order to have a stable calculation, we pose different conditions based on stability analysis. Here we have discussed the Von Neumann stability analysis which is indeed a linear stability analysis.

However, situations may arise where the amplification factor is always less than unity. These conditions are referred to as unconditionally stable. In a similar way for some procedures, we may get an amplification factor which is always greater than unity. Such methods are unconditionally unstable.

Over and above, it should be realized that such stability analysis are not really adequate for practical complex problems. In actual fluid flow problems, the stability restrictions are applied locally. The mesh is scanned for the most restrictive value of the stability limitations and the resulting minimum 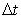is used throughout the mesh. For variable coefficients, the Von Neumann condition is only necessary but not sufficient. As such, stability criterion of a procedure is not defined by its universal applicability.

For nonlinear problems we need numerical experimentation in order to obtain stable solutions wherein the routine stability analysis will provide the initial clues to practical stability. In other words, it will give tutorial guidance.