Conservative Property
A finite-difference equation posseses conservative property if it preserves integral conservation relations of the continuum. Let us consider the vorticity transport equation
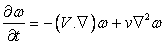 |
(9.13) |
where  is nabla or differential operator, is nabla or differential operator,
V the fluid velocity and
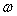 the vorticity. the vorticity.
If we integrate this over some fixed space region 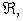 we get we get
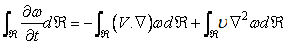 |
(9.14) |
The first term of the Eq. (9.14) can be written as
The second term of the Eq (9.14) may be expressed as
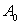 is the boundary of is the boundary of 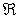 , ,
n is unit normal vector and
dA is the differential element of 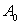 . .
The remaining term of Eq. (9.14) may be written as
As such
Finally, we can write
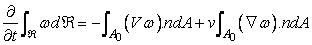 |
(9.15) |
which signifies that the time rate of accumulation of 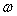 in in 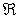 is equal to net advective flux rate of is equal to net advective flux rate of 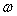 across across 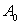 into into 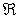 plus net diffusive flux rate of plus net diffusive flux rate of 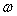 across across 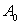 into into 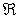 . .
The concept of conservative property is to maintain this integral relation in finite difference representation.
Congratulations, you have finished Lecture 9. To view the next lecture select it from the left hand side menu of the page or click the next button. |