Assume that the distribution of error along the x- axis is given by a Fourier series in x and the time-wise distribution is exponential in t, i.e,
 |
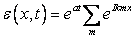(7.6) |
where I is the unit complex number and km the wave number. Since the difference is linear, when Eq. (7.6) is substituted into Eq. (7.4), the behavior of each term of the series is the same as the series itself.
Hence, let us deal with just one term of the series, and write
 |
(7.7) |
Substitute Eq. (7.7) into (7.4) to get
 |
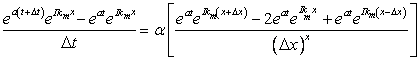(7.8) |
Divide Eq. (7.8) by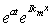 
or,
 |
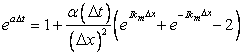(7.9) |
Recalling the identity
Eq. (7.9) can be written as
or,
 |
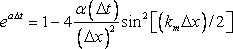(7.10) |
From Eq.(7.7), we can write
 |
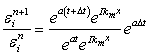(7.11) |
Combining Eqns. (7.10), (7.11) and (7.5), we have
 |
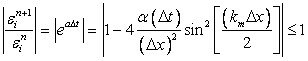(7.12) |
Eq. (7.12) must be satisfied to have a stable solution. In Eq (7.12) the factor 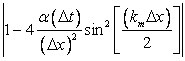 is called the amplification factor and is denoted by G.
|
