Round-off:
This is the numerical error introduced for a repetitive number of calculations in which the computer is constantly rounding the number to some decimal points.
If A= analytical solution of the partial differential equation,
D= exact solution of the finite-difference equation
N=numerical solution from a real computer with finite accuracy
Then, Discretization error = A − D = Truncation error + error introduced due to treatment of boundary condition
Round-of error 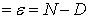
or,
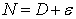 |
(7.1) |
where, 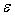 is the round-off error, which henceforth will be called “error” for convenience. is the round-off error, which henceforth will be called “error” for convenience.
The numerical solution N must satisfy the finite difference equation.
Hence from Eq. (3.4)
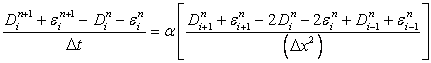 |
(7.2) |
By definition, D is the exact solution of the finite difference equation, hence it exactly satisfies
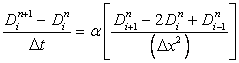 |
(7.3) |
Subtracting Eq. (2.44) from Eq. (2.43)
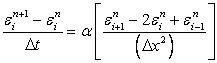 |
(7.4) |
From Equation (7.4) we see that the error 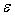 also satisfies the difference equation. also satisfies the difference equation.
If errors 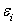 are already present at some stage of the solution of this equation, then the solution will be stable if the are already present at some stage of the solution of this equation, then the solution will be stable if the 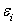 's shrink, or at least stay the same, as the solution progresses in the marching direction, i.e from step n to n+1. If the 's shrink, or at least stay the same, as the solution progresses in the marching direction, i.e from step n to n+1. If the 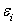 's grow larger during the progression of the solution from step n to n+1 , then the solution is unstable. Finally, it stands to reason that for a solution to be stable, the mandatory condition is 's grow larger during the progression of the solution from step n to n+1 , then the solution is unstable. Finally, it stands to reason that for a solution to be stable, the mandatory condition is
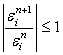 |
(7.5) |
For Eq. (3.4), let us examine under what circumstances Eq. (7.5) hold good.
|