Evaluating the inequality in Eq. (7.12), the two possible situations which must hold simultaneously are
Thus,
Since 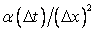 is always positive, this condition always holds. is always positive, this condition always holds.
The other condition is
Thus,
For the above condition to hold
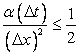 |
(7.13) |
Eq. (7.13) gives the stability requirement for which the solution of the difference Eq. (3.4) will be stable.
It can be said that for a given 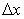 the allowed value of the allowed value of 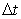 must be small enough to satisfy Eq. (7.13). For must be small enough to satisfy Eq. (7.13). For 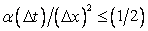 the error will not grow in subsequent time marching steps in t, and the numerical solution will proceed in a stable manner. On the contrary, if the error will not grow in subsequent time marching steps in t, and the numerical solution will proceed in a stable manner. On the contrary, if 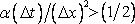 then the error will progressively become larger and the calculation will be useless. then the error will progressively become larger and the calculation will be useless.
The above mentioned analysis using Fourier series is called the Von Neumann stability analysis.
Congratulations! You have finished Lecture 7. To view the next lecture select it from the left hand side menu of the page or click the next button.
|