Time Discretization
The generalized transport equation for unsteady flows may be written as
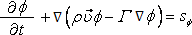 |
(40.5) |
where 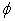 is the transported variable (i.e. the velocity components, the temperature, the concentration etc.) is the transported variable (i.e. the velocity components, the temperature, the concentration etc.) 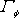 the coefficient of diffusivity and the coefficient of diffusivity and 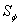 is the source term. is the source term.
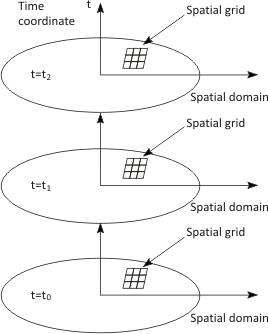
Fig. 40.1: Discretization in time coordinate
In addition to the spatial discretization a discretization in time direction is now required. Time may be regarded as an additional coordinate, therefore a spatial problem can be considered as a sequence of levels at several instants, called “time levels” (Fig. 40.1). Since time evolves in one direction, it is also called "one way" coordinate. In contrast to spatial discretization the variable values have to be known at a previous time level (starting from the given initial values). New time level are always “extrapolated” from the earlier one. Integration of Eq. (40.5) over a CV and the time interval (tn-1, tn) leads to:
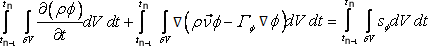 |
(40.6) |
The volume integrals are treated the same way as discussed earlier. Equation (40.5) can be written as:
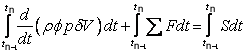 |
(40.7) |
Carrying out the time integration leads to:
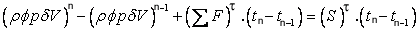 |
(40.8) |
|