The source and coefficients are assumed as average values taken at a time level 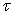 with with 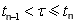 and are therefore specified by the superscript and are therefore specified by the superscript 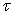 . They can be expressed by quantities taken at the time level . They can be expressed by quantities taken at the time level 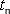 and and 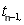 respectively. The average values in Eqn.. (40.8) may be taken as follows: respectively. The average values in Eqn.. (40.8) may be taken as follows:
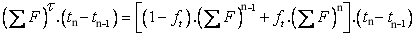
|
(40.9) |
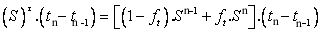 |
(40.10) |
The theoretical limiting values for the blending factor 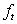 are zero and one, respectively. However, when are zero and one, respectively. However, when 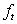 is set equal to zero the time average of the fluxes and sources are taken completely at the old time level resulting in an explicit scheme. Therefore, is set equal to zero the time average of the fluxes and sources are taken completely at the old time level resulting in an explicit scheme. Therefore, 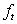 may also be chosen in the interval (0,1]. Practically, in the case of may also be chosen in the interval (0,1]. Practically, in the case of 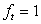 all fluxes are calculated at the new time step, resulting in a fully implicit scheme (implicit Euler scheme) with very good stability properties. There is no restriction for the time step with respect to numerical stability. The equations for steady problems result from the limit all fluxes are calculated at the new time step, resulting in a fully implicit scheme (implicit Euler scheme) with very good stability properties. There is no restriction for the time step with respect to numerical stability. The equations for steady problems result from the limit 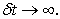
For 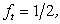 the Crank-Nicolson scheme, which is of second orde accuracy is obtained. For this scheme there exists a limiting value for the time step ensuring numerical stability, but due to the complexity of the underlying differential equation it is not possible to estimate this limiting value in advance. the Crank-Nicolson scheme, which is of second orde accuracy is obtained. For this scheme there exists a limiting value for the time step ensuring numerical stability, but due to the complexity of the underlying differential equation it is not possible to estimate this limiting value in advance.
Congratulations, you have finished Lecture 40. To view the next lecture select it from the left hand side menu of the page or click the next button. |